Question

The magnification produced by a mirror is $-1$. What does it mean?

Answer 1

Hint: In order to answer the above question, we will be studying the types of curved mirrors and we will take a look at the mirror formulae. Finally we will discuss the magnification of the image and its formula to reach our answer.

Complete step by step solution:
As we can interpret that spherical mirrors are those with curved surfaces on one of their sides that are painted. Convex mirrors are spherical mirrors with painted inward surfaces, while concave mirrors are spherical mirrors with painted outward surfaces.
Concave mirrors are often called converging mirrors because the rays converge after passing through them, while convex mirrors are called diverging mirrors because the rays diverge after passing through them.
Let's look at the formula and magnification that spherical mirrors make.
The Mirror formula describes how the focal length of a spherical mirror is related to the object distance \[\left( u \right)\]and image distance\[\left( v \right)\]. The object distance, denoted by the letter $u$, is the distance between the object and the mirror's pole. The image distance, denoted by the letter $v$, is the distance between the image and the pole of the mirror. The focal length $f$ is the distance between the main focus and the mirror's pole. The mirror formula is an expression that expresses the relationship between these three quantities and is written as:
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
For any object position, the mirror formula applies to all spherical mirrors.

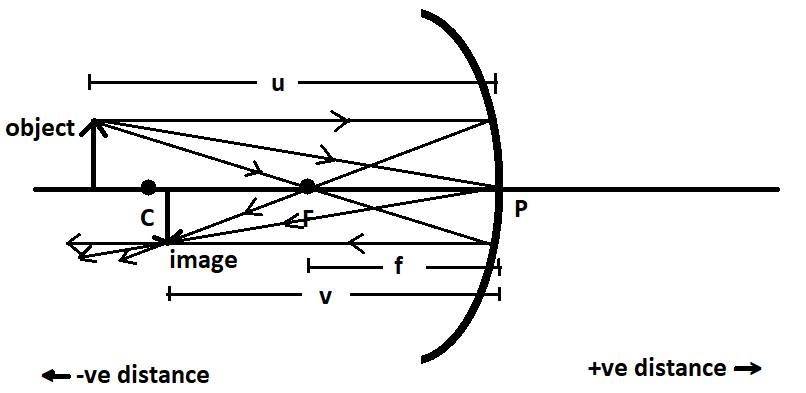
Magnification refers to the increase in image size created by spherical mirrors in comparison to the size of the object. It's the height of the image divided by the height of the object, and it's written as $m$. A spherical mirror's magnification, $m$, can be expressed as follows:
$m=\dfrac{h}{h'}$
Where $h$is the object height and $h'$is the image height.
The ratio of image distance to object distance is also known as magnification.
$m=\dfrac{v}{u}$
The object's height is always positive since it is always above the principal axis. However, depending on the type of image created, the sign for image height can change. Digital images should have a positive height, whereas real-world images should have a negative height.
From all the above information, we can interpret that if the magnification of the image is $-1$, then the following can be concluded:
> The image is formed on the left side of the mirror in the same direction of the object. Therefore the magnification is negative.
> The image formed is of the same size that of the object as the magnification is unity.
> The image formed is real and inverted.
> The negative value of magnification also suggests that the mirror was a concave mirror.
> The value of magnification also suggests that the image and the object both lie at the center of curvature of the mirror or the distance of the object and the image is twice the focal length of the mirror from the pole of the mirror.

Note:
It is very important to note that A virtual and erect image is indicated by a positive magnification magnitude. The picture is real and inverted when the magnification is negative. It is also very important to measure the object and the image distance correctly. Both the object and the image distance is measured from the pole of the mirror and it is negative and positive according to the right hand side and the left hand side of the mirror respectively.