Question

The magnetic field in a plane electromagnetic wave is given by $2\times {{10}^{-7}}\sin (0.5\times {{10}^{3}}x+1.5\times {{10}^{11}}t)$.This electromagnetic wave is
A. Visible light
B. Infrared
C. Microwave
D. Radio Wave

Answer 1

Hint: the above equation is of electromagnetic wave, by equating the above equation with the standard equation of electromagnetic wave we need to find wavelength, and by comparing it in the electromagnetic spectrum we can identify the type of waveform.

Formula used:
$E={{E}_{m}}\sin (kx+\omega t)$
$k=\dfrac{2\pi }{\lambda }$.

Complete solution:
The standard electromagnetic wave equation travelling in negative direction of x-axis is given by $E={{E}_{m}}\sin (kx+\omega t)$,

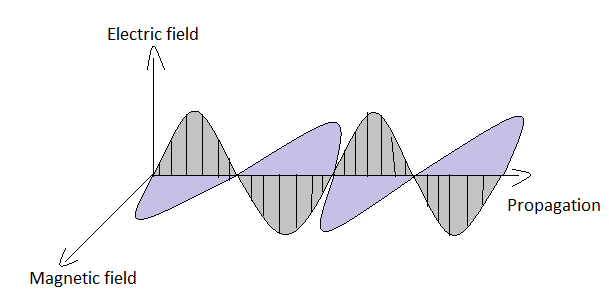
Here, ${{E}_{m}}$(amplitude), $k$(propagation constant), $\omega $(angular frequency) and $t$(time period).

Now, we know that $k=\dfrac{2\pi }{\lambda }$ and from the given equation by comparing $k=0.5\times {{10}^{3}}$ so,
$\dfrac{2\pi }{\lambda }=0.5\times {{10}^{3}}$
$\lambda =\dfrac{2\pi }{0.5\times {{10}^{3}}}=12.56\times {{10}^{-3}}m$

Electromagnetic energy travels in waves and spans a broad spectrum from very long radio waves to very short gamma rays and divided into seven different spectrum, the wavelength range of microwave is 1m to ${{10}^{-3}}m$ so our required range satisfied our wavelength.

Therefore, the answer is option C Microwave.

Additional information:
Light can be classified as a wave or particle due to its dual nature of wave-like properties and due to packets of energy called photons particle-like properties. One of the most significant properties of light is the polarization that is the electromagnetic field’s alignment.

Note:
The electric field is produced by a charged particle when a force is exerted by this electric field on other charged particles so the positive and negative charged particles accelerate In opposite direction same goes for magnetic field and electromagnetic field or wave is produced by these particles. Electromagnetic waves are the combination of the electric and magnetic fields moving in free space perpendicular to each other with the speed of light.