Question

The magnetic field at the center of a current-carrying loop of the radius $0.1m$ is $5\sqrt{5}$ times that at a point along its axis. The distance of this point from the center of the loop is
A. $0.2m$
B. $0.05m$
C. \[0.1m\]
D. $0.25m$

Answer 1

Hint: Every current-carrying conductor produces a magnetic field around its circumference. The field lines which are produced never intersect each other. The magnetic field at a point generated around a current-carrying conductor decreases with the increase in the distance of the point from the center.

As per the given data,
The radius (R) of the circle is $0.1m$ $\left( 10cm \right)$
The magnetic field at the center $\left( {{B}_{center}} \right)$ is \[~5\sqrt{5}\left( {{B}_{axis}} \right)\]

Complete answer:
The condition given in the question can be visualized as shown in the diagram below.

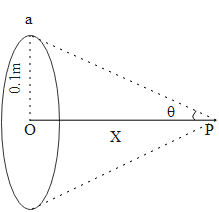
According to the Biot-Savart's Law, the magnetic field at the center of the circular loop is given as,
${{B}_{center}}=\dfrac{{{\mu }_{0}}I}{2R}$
So from the given information
${{B}_{center}}=5\sqrt{5}{{B}_{axis}}=\dfrac{{{\mu }_{0}}I}{2R}\quad ...\left( 1 \right)$
In the case of a circular conductor loop, every point of the conductor has its impact on the magnetic field at a point tangentially to the loop. The magnetic field can be divided into Cartesian coordinates x and y.

The sin component of the magnetic field will be canceled out. So the magnetic field on a point on the axis of the current-carrying loop is given by,
${{B}_{axis}}=\dfrac{{{\mu }_{0}}I{{R}^{2}}}{2{{({{R}^{2}}+{{X}^{2}})}^{\dfrac{3}{2}}}}\quad ....(2)$
Where,
$R$ Is the radius of the circle
$X$ Is the distance of the point from the center of the circle
Combining equations (1) and (2),
$\begin{align}
  & {{B}_{center}}=5\sqrt{5}\left( \dfrac{{{\mu }_{0}}I{{R}^{2}}}{2{{({{R}^{2}}+{{X}^{2}})}^{\dfrac{3}{2}}}} \right) \\
 & \Rightarrow \dfrac{{{\mu }_{0}}I}{2R}=\left( \dfrac{{{\mu }_{0}}I{{R}^{2}}}{2{{({{R}^{2}}+{{X}^{2}})}^{\dfrac{3}{2}}}} \right) \\
\end{align}$
This equation can be simplified as,
$\begin{align}
  & {{\left( 5\sqrt{5} \right)}^{2}}=\dfrac{{{\left( {{R}^{2}}+{{X}^{2}} \right)}^{3}}}{{{R}^{6}}} \\
 & \Rightarrow 125=\dfrac{{{\left( {{R}^{2}}+{{X}^{2}} \right)}^{3}}}{{{R}^{6}}} \\
 & \Rightarrow 125=1+\left( \dfrac{{{X}^{2}}}{{{R}^{2}}} \right) \\
 & \Rightarrow \dfrac{{{X}^{2}}}{{{R}^{2}}}=124 \\
 & \Rightarrow X=2R \\
\end{align}$
By putting the value of radius in $cm$
$\begin{align}
  & X=2(10) \\
 & \therefore X=20cm=0.2m \\
\end{align}$
So, from the above calculation, we can conclude that the distance of the point $P$ from the center of the loop is $0.2m$.

And the correct option which satisfies the given situation in the question is Option A.

Note:
The Biot-Savart's Law was discovered by Sir Jean-Baptiste Biot and Sir Félix Savart in 1820. This law was resultant of the discovery of magnetic induction $(B)$ which is proportional to The magnetic field $\left( H \right)$. They mathematically formulated an equation of the magnetic induction produced due to a current-carrying conductor.