Question

The liquid pressure depends upon:
(A) Depth of liquid
(B) Density of liquid
(C) Acceleration due to gravity
(D) All the above

Answer 1

Hint: To answer this question, we need to use the formula for the pressure of a liquid column. Then on investigating each of the terms present in the equation for pressure, we can get the correct answer.

Formula used: The formula which is used in solving this question is given by
 $\Rightarrow \rho = \dfrac{m}{V} $ , where $ \rho $ is the density, $ m $ is the mass, and $ V $ is the volume.

Complete step by step solution:
Let us consider a rectangular column of a liquid of density $ \rho $ as shown in the figure below. Let the base area of this rectangle be $ A $ and the depth be $ h $ . Also, let the liquid pressures acting on its top and at its bottom be $ {P_a} $ and $ {P_b} $ .

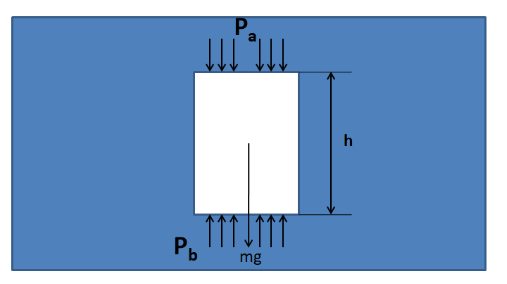
As this liquid column is kept in equilibrium inside the liquid, so the resultant forces acting in the vertical direction on it must be equal to zero. The forces which are acting in the vertical direction are
Weight $ \left( {mg} \right) $ – downwards
Force due to pressure on the top $ \left( {{P_a}A} \right) $ - downwards
Force due to pressure at the bottom $ \left( {{P_b}A} \right) $ - upwards
Now, from the vertical equilibrium of the liquid column, we have
 $\Rightarrow mg + {P_a}A - {P_b}A = 0 $
 $\Rightarrow {P_b}A - {P_a}A = mg $ (1)
Now, we know that the density of the liquid can be written as
 $\Rightarrow \rho = \dfrac{m}{V} $
So the mass of the fluid column is
 $\Rightarrow m = \rho V $
Now, we know that the volume is equal to the product of the base area and the height. So we get
 $\Rightarrow m = \rho Ah $
Substituting this in (1) we get
 $\Rightarrow {P_b}A - {P_a}A = \rho Ahg $
Dividing by $ A $ on both the sides, we get
 $\Rightarrow {P_b} - {P_a} = \rho gh $
Finally, we get the liquid pressure at the bottom as
 $\Rightarrow {P_b} = {P_a} + \rho gh $
So, as we can see from the above expression that the liquid pressure depends upon the density of the liquid $ \rho $ , the acceleration due to gravity $ g $ , and the depth of the liquid $ h $ . So the options A, B and C are correct.
Hence, the correct answer is option D, all of these.

Note:
The above expression, which has been derived as the liquid pressure is more generally known as the gauge pressure, when the pressure at the top becomes equal to the atmospheric pressure. Many pressure measuring instruments, such as the manometers, piezometers, Diaphragm Pressure Gauge are used for measuring this value.