Question

The line joining (5, 0) to (10$\cos \theta $, 10$\sin \theta $) is divided internally in the ratio 2:3 at P. If $\theta $ varies, then the locus of P is:
(a) A pair of straight lines
(b) A circle
(c) A straight line
(d) None of these

Answer 1

Hint:Let coordinates of P be $\left( x,y \right)$. Use section formula to determine the coordinates of P. section formula is given by $\left( x,y \right)$=$\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$, where m and n are the ratio in which the line segment is divided internally. Then establish the relationship between $x\text{ and }y$.

Complete step-by-step answer:
Let us assume, $({{x}_{1}},{{y}_{1}})$= (5, 0), and $({{x}_{2}},{{y}_{2}})$= (10$\cos \theta $, 10$\sin \theta $).Then, $m$ must be 2 and $n$ must be 3.

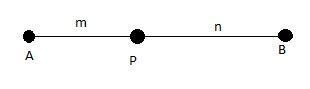
Now, let us calculate the coordinates of P.
\[\begin{align}
  & x=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n} \right) \\
 & \text{ }=\left( \dfrac{2\times 10\cos \theta +3\times 5}{2+3} \right) \\
 & \text{ }=\left( \dfrac{20\cos \theta +15}{5} \right) \\
 & \text{ }=\left( 4\cos \theta +3 \right) \\
\end{align}\]
Now,
$\begin{align}
  & y=\left( \dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right) \\
 & \text{ }=\left( \dfrac{2\times 10\sin \theta +3\times 0}{2+3} \right) \\
 & \text{ }=\left( \dfrac{20\sin \theta }{5} \right) \\
 & \text{ }=4\sin \theta \\
\end{align}$
Hence, P$\left( x,y \right)$=$\left( 4\cos \theta +3,4\sin \theta \right)$
Now,
$\begin{align}
  & x=4\cos \theta +3 \\
 & \therefore (x-3)=4\cos \theta ....................................(i) \\
\end{align}$
Also, $y=4\sin \theta .......................................(ii)$
On squaring and adding equation (i) and (ii), we get,
\[\begin{align}
  & {{(x-3)}^{2}}+{{y}^{2}}=16{{\sin }^{2}}\theta +16{{\cos }^{2}}\theta \\
 & {{(x-3)}^{2}}+{{y}^{2}}=16({{\sin }^{2}}\theta +{{\cos }^{2}}\theta ) \\
 & {{(x-3)}^{2}}+{{y}^{2}}=16 \\
 & {{(x-3)}^{2}}+{{y}^{2}}={{4}^{2}} \\
\end{align}\]
This is of the form ${{(x-a)}^{2}}+{{(y-b)}^{2}}={{r}^{2}}$, which is an equation of the circle with centre (a,b) and radius r.
Hence, option (b) is the correct answer.

Note: One may get confused in selecting the value of m and n. We don’t have to worry about that. Here, select any one of them as m and n but, remember that the side towards which we have selected ‘m’ must be denoted as coordinate $({{x}_{1}},{{y}_{1}})$ and the other side which is selected as ‘n’ must be denoted as coordinate$({{x}_{2}},{{y}_{2}})$. Then apply the section formula.