Question

The line AA’ is charged by an infinite conducting plane which is perpendicular to the plane of paper. The plane has surface density of charge $\sigma $and B is ball of mass m with a like charge of magnitude q. B is connected by string from a point on the line AA’ The tangent of angle $\left( \theta \right)$formed between the line AA’ and the string is:

$
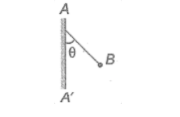
  A.\dfrac{{q\sigma }}{{2{\varepsilon _0}mg}} \\
  B.\dfrac{{q\sigma }}{{2\pi {\varepsilon _0}mg}} \\
  C.\dfrac{{q\sigma }}{{6\pi {\varepsilon _0}mg}} \\
  D.\dfrac{{q\sigma }}{{{\varepsilon _0}mg}} \\
 $

Answer 1

Hint: This problem can be solved by applying the concept of Gauss’s Law which states that, “The net electric flux through any hypothetical closed surface is equal to $\dfrac{1}{{{\varepsilon _0}}}$ times the net electric charge within that closed surface.”

Complete step-by-step answer:
Step 1: Calculate the forces acting on the ball.
Let us draw the free-body diagram of the ball as follows:

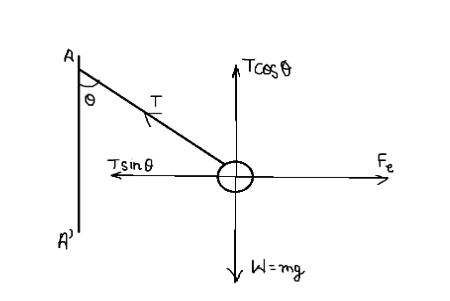
There are 3 forces acting on the ball: - Tension force, T due to the string. - Weight, $W = mg$ acting downward. - Electric force, ${F_e}$ due to the electric field due to an infinite plane.
The tension force can be resolved into 2 components as shown: $T\sin \theta \& T\cos \theta $
To calculate electric force, ${F_e}$, we have to apply Gauss’s law for an infinite plane carrying charge density of $\sigma $.
Electric field due to infinite charge carrying plane, $E = \dfrac{\sigma }{{2{\varepsilon _0}}}$
Electric force,
$
  {F_e} = qE \\
  Substituting, \\
  {F_e} = \dfrac{{q\sigma }}{{2{\varepsilon _0}}} \\
 $
By equating the forces in the free-body diagram, we get two equations –
$
  T\cos \theta = mg \\
  T\sin \theta = {F_e} \\
 $
Dividing the equations –
$
  \dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{{F_e}}}{{mg}} \\
  \tan \theta = \dfrac{{{F_e}}}{{mg}} \to \left( {\because \dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta } \right) \\
 $
Substituting for ${F_e}$ –
$
  \tan \theta = \dfrac{{{F_e}}}{{mg}} \\
  \tan \theta = \dfrac{{\left( {\dfrac{{q\sigma }}{{2{\varepsilon _0}}}} \right)}}{{mg}} \\
  \tan \theta = \dfrac{{q\sigma }}{{2{\varepsilon _0}mg}} \\
 $

Hence, the correct option is Option A.

Note: Students generally confuse while writing the horizontal and vertical components of a vector. You can use a simple and handy thumb rule as shown here:

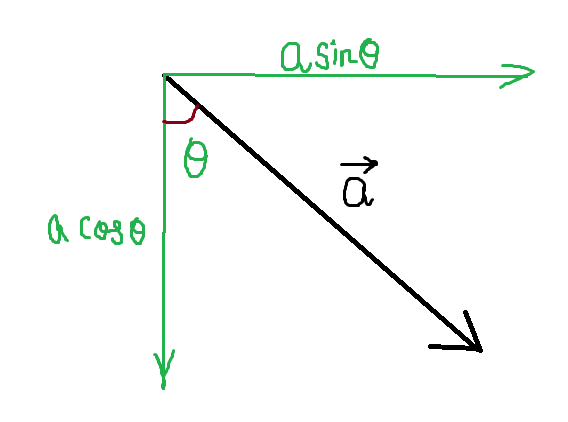
Consider a vector $\vec a$ inclined at angle $\theta $ as shown in the above figure: - The line that is attached to the angle $\theta $ is designated as $\cos \theta $. - The other line that is not attached to the angle$\theta $ is designated as $\sin \theta $