Question

The lens in an overhead projector forms an image of a point on an overhead transparency. If the screen is moved closer to the projector to keep the image on the screen in focus, the lens must be

(A) Moved Up
(B) Moved Towards Left
(C) Moved Down
(D) Moved Lens of Focal

Answer 1

Hint
To solve this sum, we just need to know the lens formula which is given by $\dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u}$ and take into consideration the image which will be formed if the mirror is removed. The sign of the distance moved by the lens will give us the answer.
In this question, we will use the formula
$\dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u}$
where, $v$ is the image distance, $u$ is the object distance and $f$ is the local length of the lens.

Complete step by step answer

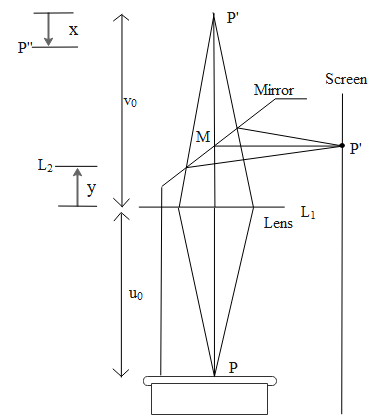
To solve this problem first, let us consider a situation where the mirror $M$ is removed. Then in that situation, the lines are extrapolated and the position of the image behind the mirror is seen as$P'$.
So therefore here as we see in the image, we consider the initial distance between the object $P$ and the lens as ${u_0}$and the distance of the point $P'$ behind the mirror from the lens as the image distance${v_0}$.
So considering the focal length of the lens to be $f$, we can write from the lens formula,
$\dfrac{1}{{{v_0}}} = \dfrac{1}{f} + \dfrac{1}{{{u_0}}}$
Now according to the problem, the screen is moved closer to the projector. This means that the image $P'$ comes closer to the lens. From the image, let us consider that the screen is moved a distance $x$ such that the new image is formed at the position $P''$.
So now to focus the image at $P''$ the lens is further moved a distance of $y$ to the new position ${{\text{L}}_{\text{2}}}$ . Now we need to find the sign of this variable $y$ which will give us the answer.
So again from this new condition, we can rewrite the lens formula again as,
$\dfrac{1}{{{v_0} - x}} = \dfrac{1}{f} + \dfrac{1}{{{u_0} - y}}$
We have already taken the variable $x$ to be positive. So we can say that,
$\dfrac{1}{{{v_0} - x}} > \dfrac{1}{{{v_0}}}$
$ \Rightarrow \dfrac{1}{f} + \dfrac{1}{{{u_0} - y}} > \dfrac{1}{{{v_0}}}$
Now we can substitute ${v_0}$from the initial lens formula as,
$\dfrac{1}{f} + \dfrac{1}{{{u_0} - y}} > \dfrac{1}{f} + \dfrac{1}{{{u_0}}}$
By canceling the $\dfrac{1}{f}$ on both the sides, we get
$\dfrac{1}{{{u_0} - y}} > \dfrac{1}{{{u_0}}}$
So this above equation is only possible when y is positive. So the Lens needs to be moved upwards.
So the correct option is A.

Note
We need to take special care of the sign conventions while doing problems in geometrical optics. In the case of the real image, if the object distance is taken as negative then the focal length and image distance are taken positively.