Question

The length of a rectangle is 14 cm more than its breadth. If the perimeter is 448 cm, then find the dimensions of the rectangle.

Answer 1

Hint: First, we will assume a variable for the breadth and the length will be 14 plus the breadth then we will apply the formula for perimeter of a rectangle that is: $2\left( length+breadth\right)$, after that we will substitute the value of the breadth, the length in terms of breadth and the value of perimeter from the question and hence, we will get the value of breadth. Finally we will add 14 to the breadth and get the length of the rectangle.

Complete step by step answer:
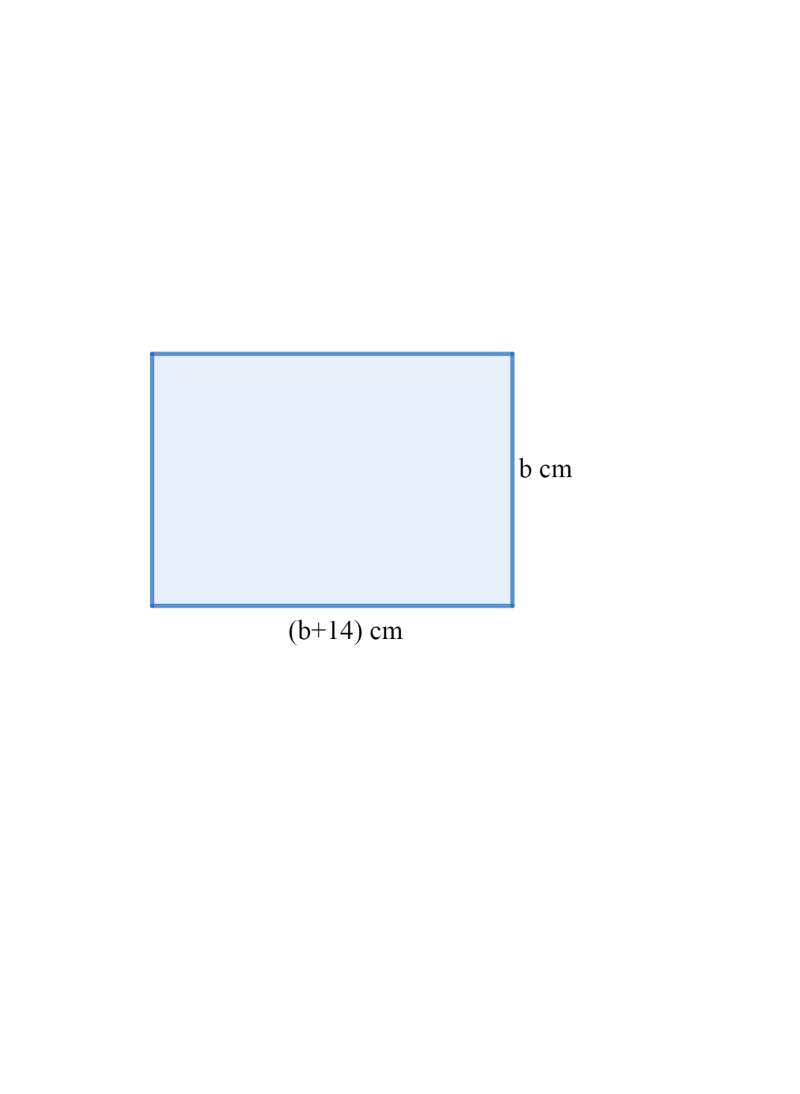
Let the breadth of the rectangle be $b$ cm.
Now it is given that the length of the rectangle is 14 cm more than the breadth therefore:
$l=b+14$ cm.

Now, it is given in the question that the perimeter of the rectangle is 448 cm.
Now we know that the perimeter of a rectangle is sum of all the sides that is:
$2\left( length+breadth\right)$
Now, we will put all the values in the formula given above, therefore we will have:
$\Rightarrow P=2\left( l+b \right)\Rightarrow 448=2\left( 14+b+b \right)\Rightarrow 448=2\left( 14+2b \right)$
Now we will take 2 on the left hand side then we will have:
$\Rightarrow \dfrac{448}{2}=\left( 14+2b \right)\Rightarrow 224=\left( 14+2b \right)$
Again we will take 14 from the right hand side to the left hand side:
$\Rightarrow 224-14=2b\Rightarrow 210=2b$
Now we will take 2 on the left hand side then we will have:
\[\Rightarrow \dfrac{210}{2}=b\Rightarrow 105=b\]
Therefore, the value of breadth is 105 cm and the length will be $l=b+14=105+14=119$ cm.

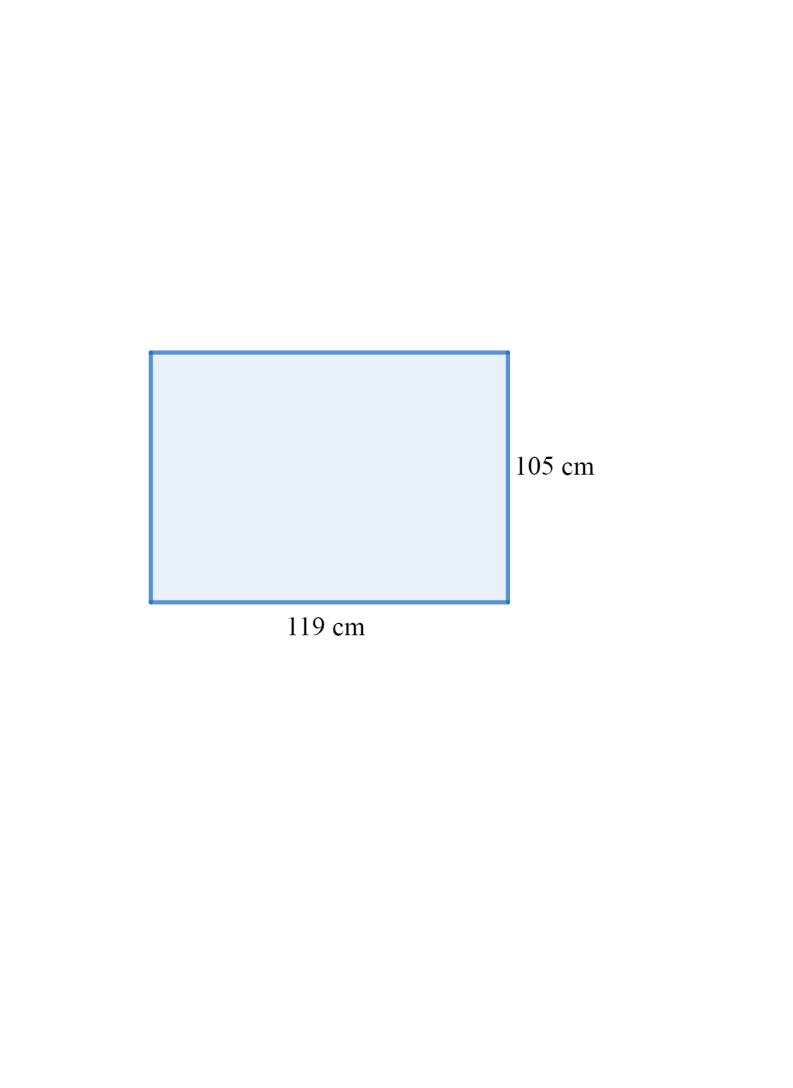
Thus, the dimension of the rectangle will be $b=105\text{ cm and }l=119\text{ cm}$.

Note: In these types of questions it is not necessary that you draw diagrams but it is anyway better. You can also do this question by taking length as $l$ and the breadth as $l-14$ , in this way you will then get:
$\begin{align}
  & \Rightarrow P=2\left( l+b \right)\Rightarrow 448=2\left( l+l-14 \right)\Rightarrow 448=2\left( 2l-14 \right) \\
 & \Rightarrow l=119\text{ cm} \\
\end{align}$
And the breadth will be $l-14=119-14=105\text{ cm}$.