Question

The length of a rectangle exceeds its breadth by 9 cm. If the length and breadth are each increased by 3 cm, then the area of the new rectangle will be $ 84c{m^2} $ more than that of the given rectangle. Find the length and breadth of the given rectangle.
A. Breadth of the rectangle is 13cm and length is 29cm.
B. Breadth of the rectangle is 5cm and length is 14cm.
C. Breadth of the rectangle is 3cm and length is 10cm.
D. Breadth of the rectangle is 8cm and length is 17cm.

Answer 1

Hint: First consider the length as l and breadth as b; l is equal to $ b + 9 $ . After increasing the length and breadth by 3cm, consider the new length and breadth as L and B. Calculate the area of the actual rectangle and the rectangle after increasing the measurements using the formula. The area of the new rectangle is $ 84c{m^2} $ more than the previous area. Using this, find the length and breadth of the rectangle.
Formula used:
Area of the rectangle with length l and breadth b is $ l \times b $

Complete step by step solution:
We are given the length of a rectangle is 9 cm more than the breadth.

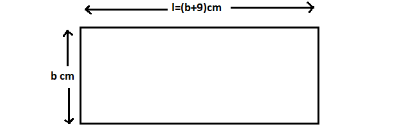
Therefore, the area of the rectangle is $ l \times b = \left( {b + 9} \right) \times b = \left( {{b^2} + 9b} \right)c{m^2} $
Then, the length and breadth of the rectangle are increased by 3 cm. Length becomes $ l + 3 $ and breadth becomes $ b + 3 $ .
Now the area of the rectangle with increased length and breadth will be $ \left( {l + 3} \right) \times \left( {b + 3} \right) $
We already know that l is equal to $ b + 9 $ , substitute it in the place of l in the above area
 $ Area = \left( {b + 9 + 3} \right) \times \left( {b + 3} \right) = \left( {b + 12} \right)\left( {b + 3} \right) $
 $ \Rightarrow Area = {b^2} + 12b + 3b + 36 = \left( {{b^2} + 15b + 36} \right)c{m^2} $
The new area is $ 84c{m^2} $ more than the previous area.
This means, $ \Rightarrow {b^2} + 15b + 36 = 84 + \left( {{b^2} + 9b} \right) $
$ \Rightarrow {b^2} + 15b + 36 = {b^2} + 9b + 84 $
$ \Rightarrow 15b + 36 = 9b + 84 $
Putting all the similar terms one side and the remaining ones other side, we get
$ \Rightarrow 15b - 9b = 84 - 36 $
$ \Rightarrow 6b = 48 $
$ \Rightarrow b = \dfrac{{48}}{6} $
$ \therefore b = 8cm $
Therefore, the breadth of the rectangle is 8 cm and the length of the rectangle is $ b + 9 = 8 + 9 = 17cm $
Hence, the correct option is Option D, breadth of the rectangle is 8cm and length is 17cm.
So, the correct answer is “Option D”.

Note: Length and breadth of a rectangle are not equal, only opposite sides are equal. When length and breadth (all the sides) are equal, then the rectangle is considered as a square. All squares are rectangles, but all rectangles are not squares.