Question

The length, breadth and height of a rectangular parallelepiped are in the ratio 6:3:1 .if the surface area of a cube is equal to the surface area of this parallelepiped; then what is the ratio of volume of cube to volume of parallelepiped?
A.1:1
B.5:4
C.7:5
D.3:2

Answer 1

Hint: We will follow the simple approach to solve this problem. First we will find the side of the cube with the help of the first condition given that is the surface area of a cube is equal to the surface area of this parallelepiped. Then we will go to find the ratio of their volumes.

Complete step-by-step answer:
Given that the length, breadth and height of a rectangular parallelepiped are in the ratio 6:3:1
Let \[l = 6x,b = 3x,h = x\]

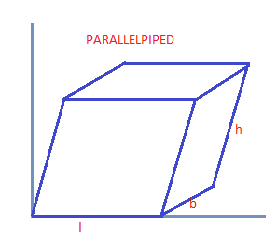
Now we know that
Total surface area of parallelepiped \[ = lateral\;surface\;area{\text{ }} + {\text{ }}2{\text{ }}base{\text{ }}area\]
\[ \Rightarrow perimeter{\text{ }}of{\text{ }}base \times height + length \times height\]
\[ \Rightarrow 2\left( {l + b} \right) \times h + 2 \times l \times b\]
Putting the values of length, breadth and height
\[
   \Rightarrow 2\left( {6x + 3x} \right) \times x + 2 \times 6x \times 3x \\
   \Rightarrow 2\left( {9x} \right) \times x + 2 \times 6x \times 3x........... \to 1 \\
\]
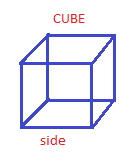
Now total surface area of cube \[ = 6 \times sid{e^2}....... \to 2\]
But it is given that the surface areas of both the diagrams are the same. Thus from 1 and 2,
\[ \Rightarrow 2\left( {9x} \right) \times x + 2 \times 6x \times 3x = 6 \times sid{e^2}\]
Dividing the above equation by 2
\[ \Rightarrow \left( {9x} \right) \times x + 6x \times 3x = 3 \times sid{e^2}\]
Multiplying the terms
\[ \Rightarrow 9{x^2} + 18{x^2} = 3 \times sid{e^2}\]
\[ \Rightarrow 27{x^2} = 3 \times sid{e^2}\]
Dividing both sides by 3
\[ \Rightarrow 9{x^2} = sid{e^2}\]
Taking square root on both sides
\[ \Rightarrow 3x = side\]
This gives the side of the cube.
Now let’s proceed towards the volume.
\[\dfrac{{V\left( {cube} \right)}}{{V\left( {parallelepiped} \right)}} = \dfrac{{sid{e^3}}}{{l \times b \times h}}\]
Substituting the values
\[ \Rightarrow \dfrac{{{{\left( {3x} \right)}^3}}}{{6x \times 3x \times x}}\]
\[ \Rightarrow \dfrac{{27{x^3}}}{{18{x^3}}}\]
Dividing both numerator and denominator by 9 and cancelling the \[{x^3}\] term.
\[ \Rightarrow \dfrac{3}{2}\]
Here is the ratio of volumes.
\[\dfrac{{V\left( {cube} \right)}}{{V\left( {parallelpiped} \right)}} = \dfrac{3}{2}\]
So the correct option is D.
Note: Here only the most important thing students generally do wrong is the ratio of the quantities in the way they are asked. It means which quantity is in numerator and which in denominator. Also note that we are given the ratio of dimensions which are taken here with x.