
The length and breadth of a rectangular field are 120 m and 80 m respectively. Inside the field, a park of 12 m width is made around the field. The area of the part is?
A.3224 m
B.7344 m
C.2256 m
D.4224 m
Answer
529.2k+ views
Hint: First we will use the formula of area of a rectangular field,
Complete step-by-step answer:
We are given that the length and breadth of a rectangular field are 120 m and 80 m respectively and inside the field, a park of 12 m width is made around the field.
Let us assume that the ABEF is the park and DOPC is the rectangular field.
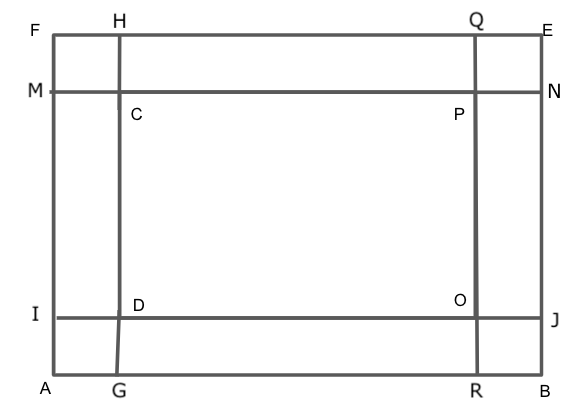
So, we have the length AB and EF is 120 m and the length AF and BE is 80 m.
Since we are given that the width of the park is 12 m, then we will have the value of DG, PN, QP, MC, DI, AI, EN, HC and MF is 12 m.
Now we will compute the dimensions of the new field.
We know that the lengths of DO and PC are equal and the lengths of OP and CD are equal.
Computing the length of DO by substituting the value of AB and DI in
Thus, the length of DO and PC is 96 m.
Computing the length of OP by substituting the value of AF and AI in
Thus, the length of OP and AF is 56 m.
We know that the formula of the area of a rectangular field,
Calculating the area of original park ABEF, we get
Calculating the area of new park DOPC, we get
Finding the area of the park by subtracting the area of DOPC from ABEF, we get
Hence, option D is correct.
Note: In solving these types of questions, students should remember that the area of any shape is the product of the length of all its sides. And there are four sides in a rectangle out of which opposite sides are equal and adjacent sides are different. And the adjacent sides of the rectangle are known as length and breadth. So students should know that the width is also a breadth. So, the formula will be the same as is given for the area of a rectangular.
Complete step-by-step answer:
We are given that the length and breadth of a rectangular field are 120 m and 80 m respectively and inside the field, a park of 12 m width is made around the field.
Let us assume that the ABEF is the park and DOPC is the rectangular field.

So, we have the length AB and EF is 120 m and the length AF and BE is 80 m.
Since we are given that the width of the park is 12 m, then we will have the value of DG, PN, QP, MC, DI, AI, EN, HC and MF is 12 m.
Now we will compute the dimensions of the new field.
We know that the lengths of DO and PC are equal and the lengths of OP and CD are equal.
Computing the length of DO by substituting the value of AB and DI in
Thus, the length of DO and PC is 96 m.
Computing the length of OP by substituting the value of AF and AI in
Thus, the length of OP and AF is 56 m.
We know that the formula of the area of a rectangular field,
Calculating the area of original park ABEF, we get
Calculating the area of new park DOPC, we get
Finding the area of the park by subtracting the area of DOPC from ABEF, we get
Hence, option D is correct.
Note: In solving these types of questions, students should remember that the area of any shape is the product of the length of all its sides. And there are four sides in a rectangle out of which opposite sides are equal and adjacent sides are different. And the adjacent sides of the rectangle are known as length and breadth. So students should know that the width is also a breadth. So, the formula will be the same as is given for the area of a rectangular.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

How many ounces are in 500 mL class 8 maths CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

When people say No pun intended what does that mea class 8 english CBSE

Give me the opposite gender of Duck class 8 english CBSE




