
The least and the greatest distances of the point $\left( {10,7} \right)$from the circle ${x^2} + {y^2} - 4x - 2y - 20 = 0$ are
A. 10,5
B. 15,20
C. 12,16
D. 5,15
Answer
578.7k+ views
Hint: We can check where the point lies with respect to the circle by putting the point in the equation of the line. Then we can find the radius and center of the circle from its equation. We can find the distance from the origin to the point. Then we can find the least and greatest distance from the radius the distance between the point and the center.
Complete step by step answer:
We have the circle ${x^2} + {y^2} - 4x - 2y - 20 = 0$. We can substitute the point $\left( {10,7} \right)$ in the equation of the circle, we get,
$\begin{gathered}
x = 10 \\
y = 7 \\
\end{gathered} $
$\begin{gathered}
{x^2} + {y^2} - 4x - 2y - 20 = {10^2} + {7^2} - 4 \times 10 - 2 \times 7 - 20 \\
= 100 + 49 - 40 - 14 - 20 \\
= 75 \\
\end{gathered} $
As the value is greater than 0, the point$\left( {{\text{10,7}}} \right)$ lies outside the circle.
Now we can find the center and radius of the equation. From the equation, we get,
${x^2} + {y^2} - 4x - 2y - 20 = 0$
On expanding the coefficients of x and y, we get,
\[ \Rightarrow {x^2} + {y^2} - 2 \times 2 \times x - 2 \times 1 \times y + {2^2} + {1^2} - 4 - 1 - 20 = 0\]
On rearranging, we get,
\[ \Rightarrow \left( {{x^2} - 2 \times 2 \times x + {2^2}} \right) + \left( {{y^2} - 2 \times 1 \times y + {1^2}} \right) - 4 - 1 - 20 = 0\]
Using the algebraic identity ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$, we get,
${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} - 25 = 0$
Thus equation of circle in standard form is ,
${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = {5^2}$
We know that for a circle with radius r and centre $\left( {h,k} \right)$, standard equation is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
So, from the equation, we get the centre is $\left( {{\text{2,1}}} \right)$ and radius is 5 units.
The distance to the point $\left( {{\text{10,7}}} \right)$ from the center of the circle $\left( {{\text{2,1}}} \right)$ is given by,
$d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
On substituting the points, we get,
$d = \sqrt {{{\left( {10 - 2} \right)}^2} + {{\left( {7 - 1} \right)}^2}} $
$\begin{gathered}
= \sqrt {{8^2} + {6^2}} \\
= \sqrt {64 + 36} \\
\end{gathered} $
$\begin{gathered}
= \sqrt {100} \\
= 10{\text{ }}units \\
\end{gathered} $
Now we have the point 10 units away from the centre.
Now we can draw a figure with the details we found out.
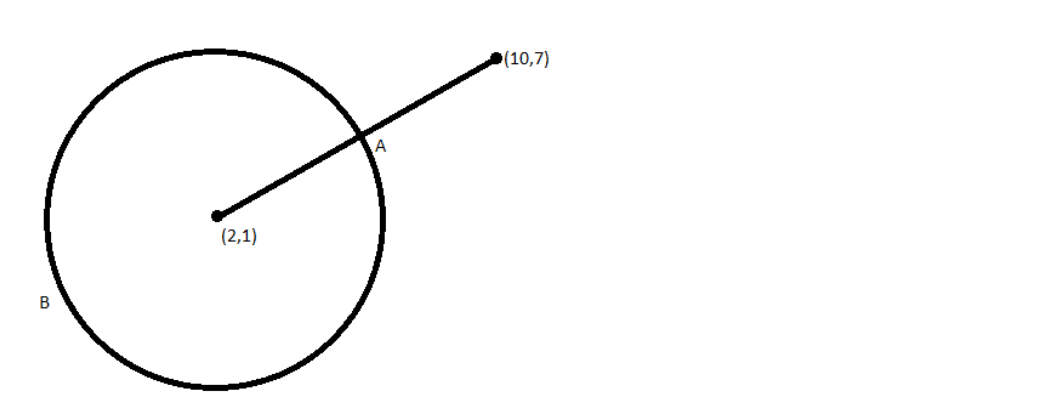
From the figure, the shortest distance to the point is from point A. So, the least distance is given by the difference between the radius and the distance to the point from the center. The least distance is given by,
$l = d - r = 10 - 5 = 5{\text{ }}units$
Similarly, the largest distance will the sum of the radius and the distance to the point from the center. It is given by,
$g = d + r = 10 + 5 = 15{\text{ }}units$
Therefore, the least and the greatest distances of the point $\left( {10,7} \right)$ from the circle are 5 units and 15 units.
So, the correct answer is option D.
Note: When we put a point to a circle’s equation, the point lies on the circle if the equation becomes zero. The point lies outside the circle if the equation gives a value greater than zero and inside the circle if the equation gives value less than zero. Drawing a figure helps us to understand the least and greatest distance from the point.
Complete step by step answer:
We have the circle ${x^2} + {y^2} - 4x - 2y - 20 = 0$. We can substitute the point $\left( {10,7} \right)$ in the equation of the circle, we get,
$\begin{gathered}
x = 10 \\
y = 7 \\
\end{gathered} $
$\begin{gathered}
{x^2} + {y^2} - 4x - 2y - 20 = {10^2} + {7^2} - 4 \times 10 - 2 \times 7 - 20 \\
= 100 + 49 - 40 - 14 - 20 \\
= 75 \\
\end{gathered} $
As the value is greater than 0, the point$\left( {{\text{10,7}}} \right)$ lies outside the circle.
Now we can find the center and radius of the equation. From the equation, we get,
${x^2} + {y^2} - 4x - 2y - 20 = 0$
On expanding the coefficients of x and y, we get,
\[ \Rightarrow {x^2} + {y^2} - 2 \times 2 \times x - 2 \times 1 \times y + {2^2} + {1^2} - 4 - 1 - 20 = 0\]
On rearranging, we get,
\[ \Rightarrow \left( {{x^2} - 2 \times 2 \times x + {2^2}} \right) + \left( {{y^2} - 2 \times 1 \times y + {1^2}} \right) - 4 - 1 - 20 = 0\]
Using the algebraic identity ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$, we get,
${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} - 25 = 0$
Thus equation of circle in standard form is ,
${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = {5^2}$
We know that for a circle with radius r and centre $\left( {h,k} \right)$, standard equation is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
So, from the equation, we get the centre is $\left( {{\text{2,1}}} \right)$ and radius is 5 units.
The distance to the point $\left( {{\text{10,7}}} \right)$ from the center of the circle $\left( {{\text{2,1}}} \right)$ is given by,
$d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
On substituting the points, we get,
$d = \sqrt {{{\left( {10 - 2} \right)}^2} + {{\left( {7 - 1} \right)}^2}} $
$\begin{gathered}
= \sqrt {{8^2} + {6^2}} \\
= \sqrt {64 + 36} \\
\end{gathered} $
$\begin{gathered}
= \sqrt {100} \\
= 10{\text{ }}units \\
\end{gathered} $
Now we have the point 10 units away from the centre.
Now we can draw a figure with the details we found out.
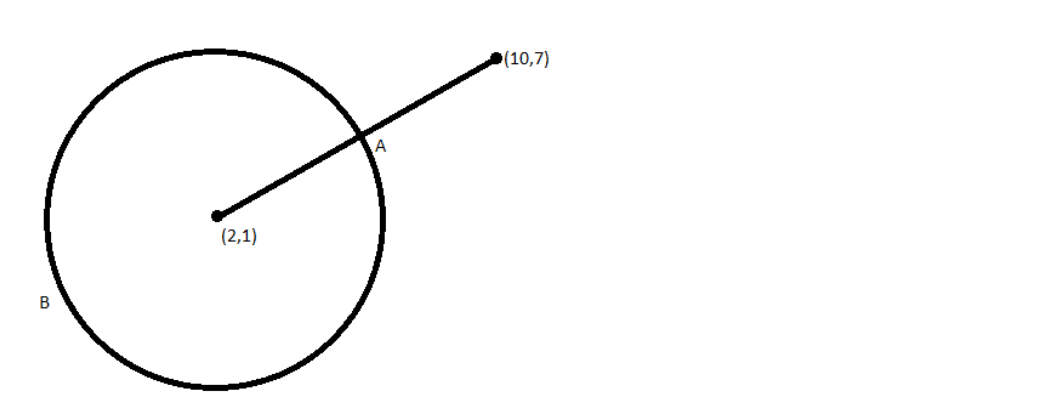
From the figure, the shortest distance to the point is from point A. So, the least distance is given by the difference between the radius and the distance to the point from the center. The least distance is given by,
$l = d - r = 10 - 5 = 5{\text{ }}units$
Similarly, the largest distance will the sum of the radius and the distance to the point from the center. It is given by,
$g = d + r = 10 + 5 = 15{\text{ }}units$
Therefore, the least and the greatest distances of the point $\left( {10,7} \right)$ from the circle are 5 units and 15 units.
So, the correct answer is option D.
Note: When we put a point to a circle’s equation, the point lies on the circle if the equation becomes zero. The point lies outside the circle if the equation gives a value greater than zero and inside the circle if the equation gives value less than zero. Drawing a figure helps us to understand the least and greatest distance from the point.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE

Which is the longest day and the shortest night in class 9 social science CBSE

Which are the Top 10 Largest States of India?

Why did Aurangzeb ban the playing of the pungi Answer class 9 english CBSE

Distinguish between the following Ferrous and nonferrous class 9 social science CBSE




