Question

The LCM of $30$ and $45$ is:
$\left( {\text{A}} \right){\text{ 15}}$
$\left( {\text{B}} \right){\text{ 30}}$
$\left( {\text{C}} \right){\text{ 45}}$
$\left( {\text{D}} \right){\text{ 90}}$

Answer 1

Hint: In this question, we have to find the least common multiple of the numbers. We can easily solve the given number by applying a prime factorisation method. In the prime factorization method, first we have to find the factors of the given numbers. Then, we need to find out the prime factors for the given numbers separately. Multiplying the prime factors we will get the required answer.

Complete step by step answer:
It is given that the number is $30$ and $45$
Now we have to find out the prime factor of the given number.
Prime factors of 30 are $2$, $3$ and $5$.
If we express it in exponential form we get-
$30 = 2_{}^1 \times 3_{}^1 \times 5_{}^{}$
Also, we have to find out the prime factors of $45$ are $3$ and $5$.
If we express it in exponential form we get-
$45 = 3_{}^2 \times 5_{}^1$
In order to find out the LCM of $30$ and $45$,
We have to need multiply, that is the highest exponent prime factors
So we can write it as,
Least common multiple (LCM) of ($30,45$)$ = 2_{}^1 \times 3_{}^2 \times 5_{}^1$
On multiplying the terms and we get,
$ = 90$
Hence the Least common multiple (LCM) of ($30,45$) is $90$
$\therefore $ The required answer was found.

Here, the correct option is \[D\].

Note: We have solved this question by applying the prime factorization method. But there is another method where first we have to find out the highest common factor and then we have to multiply the two numbers which are given in the question and have to divide it by the highest common factor.
Let the given numbers are $30$ and $45$,
Finding the common factors of the given number,

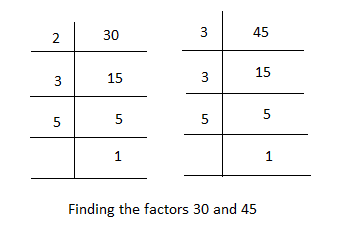
Factors of $30 = 2 \times 3 \times 5$
Factors of $45 = 3 \times 3 \times 5$
Highest common factor (HCF) of $30$ and $45$ is $3 \times 5 = 15$
The formula of LCM using HCF is $LCM\left( {a,b} \right) = \dfrac{{\left( {a \times b} \right)}}{{HCF\left( {a,b} \right)}}$
Applying on that formula we get,
$LCM\left( {30,45} \right) = \dfrac{{\left( {30 \times 45} \right)}}{{HCF\left( {30,45} \right)}}$
Substituting the Highest common factor of $30$ and $45$,
$LCM\left( {30,45} \right) = \dfrac{{1350}}{{15}}$
Simplifying we get,
$LCM\left( {30,45} \right) = 90$
Least common multiple of $30$ and $45$ is $90$.
Both the methods are correct and you can do whichever you find easy.
Least common multiple (LCM) is a technique which is used to find out the smallest common multiple between two or more numbers.