Question

The kinetic energy (in KeV) of the alpha particle, when the nucleus $_{84}^{210}Po$ at rest undergoes alpha decay, is

\[\begin{align}
  & \text{A}\text{. 5319} \\
 & \text{B}\text{. 5422} \\
 & \text{C}\text{. 5707} \\
 & \text{D}\text{. 5818} \\
\end{align}\]

Answer 1

Hint: Alpha decay is the process an unstable nucleus goes under in order to become more stable. Write the equation for the alpha decay of the given particle and then find the value of energy Q, using the given table. Then apply the law of conservation of momentum to find the value of kinetic energy of the alpha particle.

Formula Used:
The equation for alpha decay: \[{}_{Z}^{A}X\to {}_{Z-2}^{A-4}Y+{}_{2}^{4}He+Q\]
The kinetic energies, $k{}_{1}+{{k}_{2}}=Q$

Complete step by step solution:
Alpha decay is a process in which an unstable nucleus transforms itself into a new nucleus by emitting an alpha particle i.e., a helium nucleus${}_{2}^{4}H$.
Since an$\alpha -\text{particle}$ has two protons and two neutrons, so after the decay, the parent nucleus is transformed into a daughter nucleus with a mass number smaller by 4 and the atomic number smaller by 2.
The equation for alpha decay can be expressed as follows:
\[{}_{Z}^{A}X\to {}_{Z-2}^{A-4}Y+{}_{2}^{4}He+Q\]
Here Q is the energy released in the process and can be determined from Einstein’s mass-energy relation which is given by:
$Q=\left[ {{m}_{X}}-{{m}_{Y}}-{{m}_{He}} \right]{{c}^{2}}$
where ${{m}_{X}},{{m}_{Y}}\text{ and }{{m}_{He}}$ are the masses of the parent nucleus X, daughter nucleus Y, and the $\alpha -\text{particle}$respectively. The energy Q is shared by the daughter nucleus Y and the $\alpha -\text{particle}$. As the parent nucleus is at rest before its decay, the $\alpha -\text{particle}$are emitted with fixed energy. This energy in turn can be calculated by applying the laws of conservation of energy and momentum.
So, we know that the equation for alpha decay for the given nucleus will be given by:
\[{}_{84}^{210}Po\to {}_{82}^{206}Pb+{}_{2}^{4}He+Q\]
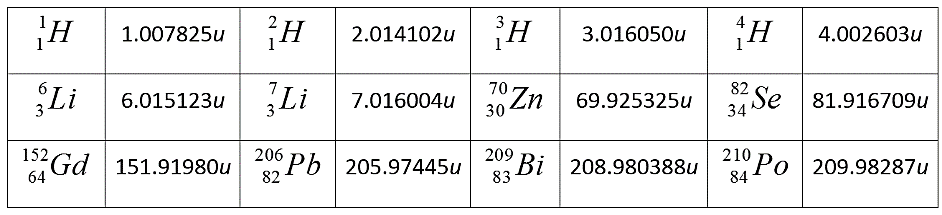
Substituting values from the given table in the above equation, we get:
\[\begin{align}
  & Q=\left( 209.982876-4.002603-205.97455 \right){{C}^{2}} \\
 & \Rightarrow \left( 209.982876-209.977153 \right){{C}^{2}} \\
 & \therefore Q=5.422MeV\cdots \cdots \cdots \cdots \cdots \left( 1 \right) \\
\end{align}\]
The momentum of the alpha particle remains conserved when the nucleus undergoes the alpha decay, this can be given as:
$\sqrt{2{{m}_{\alpha }}{{k}_{1}}}=\sqrt{2{{m}_{Pb}}{{k}_{2}}}$
Squaring both sides of the equation, we get:
\[\begin{align}
  & {{m}_{\alpha }}{{k}_{1}}={{m}_{Pb}}{{k}_{2}} \\
 & \Rightarrow 4{{k}_{1}}=206{{k}_{2}} \\
 & \Rightarrow {{k}_{1}}=\dfrac{206}{4}{{k}_{2}} \\
 & \Rightarrow {{k}_{2}}=\dfrac{4}{206}{{k}_{1}} \\
 & \therefore {{k}_{2}}=\dfrac{2}{103}{{k}_{1}}\cdots \cdots \cdots \cdots \left( 2 \right) \\
\end{align}\]
Also, we know that
\[\begin{align}
  & {{k}_{1}}+{{k}_{2}}=Q \\
 & \Rightarrow {{k}_{1}}+{{k}_{2}}=5.422MeV\text{ }\left[ \because \text{from equation (1)} \right] \\
\end{align}\]
Substituting the value of \[{{k}_{2}}\]from equation (2) in the above equation, we get:
\[\begin{align}
  & {{k}_{1}}+\dfrac{2}{103}{{k}_{1}}=5.422MeV \\
 & \Rightarrow \dfrac{103+2}{103}{{k}_{1}}=5.422MeV \\
 & \Rightarrow \dfrac{105}{103}{{k}_{1}}=5.422MeV \\
 & \Rightarrow 105{{k}_{1}}=558.466MeV \\
 & \Rightarrow {{k}_{1}}=\dfrac{558.466}{105}MeV \\
 & \Rightarrow {{k}_{1}}=5.319MeV \\
 & \therefore {{k}_{1}}=5319KeV \\
\end{align}\]
Therefore, the correct option is A. i.e., the kinetic energy of the alpha particle, when the nucleus $_{84}^{210}Po$ at rest undergoes alpha decay, is \[5319KeV\].

Note: An $\alpha -\text{particle}$ may exist as an entity, i.e., as an already formed inside the nucleus before it escapes from the nucleus. This alpha particle is in a state of constant motion inside the nucleus with a speed of about ${{10}^{7}}m{{s}^{-1}}$.