
The internal dimensions of the box are 1.2 m, 80 cm and 50 cm. How many cubes each of edge 7 cm can be packed in the box with faces parallel to the sides of the box .Also find the empty space left in the box.
A.$1758,143{\text{ c}}{{\text{m}}^3}$
B.$1399,143{\text{ c}}{{\text{m}}^3}$
C.$1638,143{\text{ c}}{{\text{m}}^3}$
D.$1589,143{\text{ c}}{{\text{m}}^3}$
Answer
568.5k+ views
Hint: The Volume of the bigger cuboidal box should be divided by the volume of the smaller cubical box. Then the volume of the total number of complete boxes which can be accommodated in the box should be subtracted from the volume of the bigger cuboidal box to obtain the empty space.
Complete step-by-step answer:
Given information
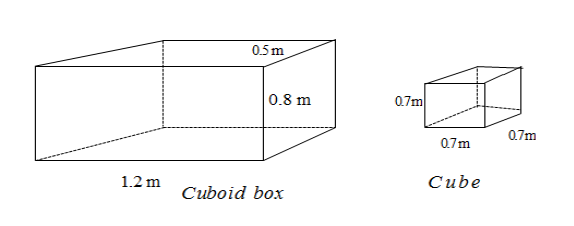
The dimensions of the cuboidal box are as follows,
Length of the box ,
$
l = 1.2{\text{ m}} \\
l = 1.2 \times 100{\text{ cm}} \\
l{\text{ = 120 cm}} \\
$
Breadth of the box,
\[b = 80{\text{ cm}}\]
Height of the box,
\[h = 50{\text{ cm}}\]
Volume of the bigger cuboidal box is given by,
$\Rightarrow {V_1} = l \times b \times h \cdots \left( 1 \right)$
Substitute the value of $l,b$ and $h$ in equation (1), we get
$
\Rightarrow {V_1} = 120 \times 80 \times 50 \\
\Rightarrow {V_1} = 480000{\text{ c}}{{\text{m}}^3} \\
$
The edge of the cubical box is,
$\Rightarrow a = 7{\text{ cm}}$
The volume of the cube is given by,
$\Rightarrow {V_2} = {a^3} \cdots \left( 2 \right)$
Substitute the value of in equation (2), we get
$
\Rightarrow {V_1} = {\left( 7 \right)^3} \\
\Rightarrow {V_1} = 343{\text{ c}}{{\text{m}}^3} \\
$
The number of smaller cubical boxes that can be accommodated in the bigger cuboidal box is given by,
$\Rightarrow n = \dfrac{{{V_1}}}{{{V_2}}} \cdots \left( 3 \right)$
Substitute the value if ${V_1}$ and ${V_2}$ in equation (3), we get
$
\Rightarrow n = \dfrac{{480000}}{{343}} \\
\Rightarrow n = 1399.417 \\
$
The complete boxes that can be accommodated in the box is, $n = 1399$.
It is quite evident that the cubical box does not fully occupy the cuboidal box. It is because the value of is rounded off to a greatest integer. The part 0.417 corresponds to the empty space in the cuboidal box.
The empty space is given by,
$\Rightarrow E = {V_1} - n{V_2} \cdots \left( 4 \right)$
Substitute the value of ${V_1} = 480000$ ,${V_2} = 343$ and $n = 1399$ in equation (4), we get
$
\Rightarrow E = 480000 - 1399 \times 343 \\
\Rightarrow E = 143{\text{ c}}{{\text{m}}^3} \\
$
Thus, the number of boxes are $n = 1399$ and the empty space is , $E = 143{\text{ c}}{{\text{m}}^3}$ .
Note: The important steps are
To calculate the number boxes that can be accommodated is calculated by, by dividing the volume of the bigger box from the volume of the cubical box.
The empty space arises because the small cubical box completely fills the entire bigger cuboidal boxes.
The number of complete boxes is rounded off to the nearest greatest integer.
The greatest integer of x returns the value which is less than or equal to x.
For instance,
$
\left[ {3.4} \right] = 3 \\
\left[ {4.1} \right] = 4 \\
$
Complete step-by-step answer:
Given information

The dimensions of the cuboidal box are as follows,
Length of the box ,
$
l = 1.2{\text{ m}} \\
l = 1.2 \times 100{\text{ cm}} \\
l{\text{ = 120 cm}} \\
$
Breadth of the box,
\[b = 80{\text{ cm}}\]
Height of the box,
\[h = 50{\text{ cm}}\]
Volume of the bigger cuboidal box is given by,
$\Rightarrow {V_1} = l \times b \times h \cdots \left( 1 \right)$
Substitute the value of $l,b$ and $h$ in equation (1), we get
$
\Rightarrow {V_1} = 120 \times 80 \times 50 \\
\Rightarrow {V_1} = 480000{\text{ c}}{{\text{m}}^3} \\
$
The edge of the cubical box is,
$\Rightarrow a = 7{\text{ cm}}$
The volume of the cube is given by,
$\Rightarrow {V_2} = {a^3} \cdots \left( 2 \right)$
Substitute the value of in equation (2), we get
$
\Rightarrow {V_1} = {\left( 7 \right)^3} \\
\Rightarrow {V_1} = 343{\text{ c}}{{\text{m}}^3} \\
$
The number of smaller cubical boxes that can be accommodated in the bigger cuboidal box is given by,
$\Rightarrow n = \dfrac{{{V_1}}}{{{V_2}}} \cdots \left( 3 \right)$
Substitute the value if ${V_1}$ and ${V_2}$ in equation (3), we get
$
\Rightarrow n = \dfrac{{480000}}{{343}} \\
\Rightarrow n = 1399.417 \\
$
The complete boxes that can be accommodated in the box is, $n = 1399$.
It is quite evident that the cubical box does not fully occupy the cuboidal box. It is because the value of is rounded off to a greatest integer. The part 0.417 corresponds to the empty space in the cuboidal box.
The empty space is given by,
$\Rightarrow E = {V_1} - n{V_2} \cdots \left( 4 \right)$
Substitute the value of ${V_1} = 480000$ ,${V_2} = 343$ and $n = 1399$ in equation (4), we get
$
\Rightarrow E = 480000 - 1399 \times 343 \\
\Rightarrow E = 143{\text{ c}}{{\text{m}}^3} \\
$
Thus, the number of boxes are $n = 1399$ and the empty space is , $E = 143{\text{ c}}{{\text{m}}^3}$ .
Note: The important steps are
To calculate the number boxes that can be accommodated is calculated by, by dividing the volume of the bigger box from the volume of the cubical box.
The empty space arises because the small cubical box completely fills the entire bigger cuboidal boxes.
The number of complete boxes is rounded off to the nearest greatest integer.
The greatest integer of x returns the value which is less than or equal to x.
For instance,
$
\left[ {3.4} \right] = 3 \\
\left[ {4.1} \right] = 4 \\
$
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is the Full Form of ISI and RAW

Distinguish between Conventional and nonconventional class 9 social science CBSE

What were the main changes brought about by the Bolsheviks class 9 social science CBSE

Differentiate between the Western and the Eastern class 9 social science CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE

Give 5 examples of refraction of light in daily life




