Question

The image of an object formed by a mirror is real, inverted and is of magnification $ - 1$ . If the image is at the distance of $30\,cm$ from the mirror, where is the object placed? Find the position of the image if the object is now moved $20\,cm$ towards the mirror. What is the nature of the obtained? Justify your answer with the help of a ray diagram.

Answer 1

Hint: Use the magnification formula, to find the distance of the object from the mirror. Substitute the values in the mirror formula, to obtain the focal length. After bringing the object towards the mirror calculate the image distance from the mirror formula.

Formula used:
(1) The magnification of the mirror is given by
$m = \dfrac{v}{u}$
Where $m$ is the magnification of the mirror, $v$ is the distance of the image from the mirror and $u$ is the distance of the object from the mirror.
(2) The mirror formula is given by
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Where $f$ is the focal length of the mirror.

Complete step by step solution:
It is given that the Image formed by the mirror is real and possesses the magnification as $ - 1$.
Distance of the image from the mirror, $v = 30\,cm$
The distance moved by the object towards the mirror, $d = 20\,cm$
Using the formula of the magnification, we get
$m = \dfrac{v}{u}$
Substituting the known values in it, we get
$\Rightarrow - 1 = \dfrac{{40}}{u}$
By simplification, we get
$\Rightarrow u = - 40$
The above value shows that the object is at a distance of $40\,cm$ from the mirror. Since the object and the image distance from the mirror is the same, the image formed will be real.
Let us use the mirror formula,
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
Substituting the distance of the object and the image from the mirror in the above formula
$\Rightarrow \dfrac{1}{f} = - \dfrac{1}{{40}} - \dfrac{1}{{40}}$
By simplification of the above equation, we get
$\Rightarrow f = - 20$
After moving the object towards the mirror, it becomes $f = - 20$ and $u = - 20$ . Substituting both in the mirror formula,
$\Rightarrow \dfrac{1}{{ - 20}} = \dfrac{1}{{ - 20}} + \dfrac{1}{v}$
By further simplification of the above equation, we get
$\Rightarrow v = \dfrac{1}{0} = \infty $

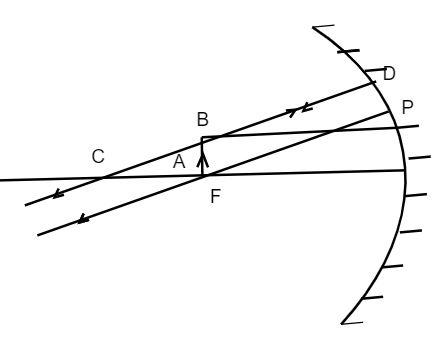
The image of the object is at infinity. But when the object comes towards the mirror, then the image will be at the focus of the mirror.

Note: Remember that if the distance of the object and the distance of the image are equal, then the object formed will be real. If the object is far away and the image distance is small then the image formed is upright. When the object is near the mirror and the image is at infinity, then the image formed is virtual.