Question

The horizontal distance between two poles is 15 m. The angle of depression of the top of the first pole as seen from the top of the second pole is 30 degree. If the height of the second pole is 24 m, find the height of the first pole. ($\sqrt{3}$ = 1.732)

Answer 1

Hint:We will take the help of the formula $\tan \left( \alpha \right)=\dfrac{Perpendicular}{Base}$ and the value of $\tan \left( {{30}^{\text{o}}} \right)=\dfrac{1}{\sqrt{3}}$ to solve the question. For further solving we will substitute the value of $\sqrt{3}$ = 1.732 into the value of height to get the accurate answer.

Complete step-by-step answer:
The required diagram for the question is shown below.

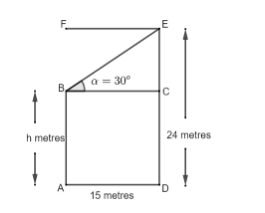
We will consider the lines AB and ED be the two poles with height h metres and 24 metres respectively. The poles have a distance of 15 metres between them. As we can clearly see that AB = CD therefore CD is also h metres. Now we will find the height of EC. Since, ED = EC + CD therefore, we will have 24 metres = EC + h metres. This results into EC = (24 – h) metres.
Similarly as ABCD is a square, so we will have the value of the side BC = AD which is 15 metres. According to the question the angle of depression given here is ${{30}^{\text{o}}}$. Now, we will apply the trigonometric formula $\tan \left( \alpha \right)=\dfrac{Perpendicular}{Base}$ to the triangle $\Delta EBC$. Thus we can now have a perpendicular side as EC = (24 – h) metres and Base is BC = 15 metres. Also, we have that $\alpha ={{30}^{\text{o}}}$ thus, we get $\tan \left( {{30}^{\text{o}}} \right)=\dfrac{24-h\,\text{metres}}{15\,\text{metres}}$.
As the value of $\tan \left( {{30}^{\text{o}}} \right)=\dfrac{1}{\sqrt{3}}$ therefore, we get
$\begin{align}
  & \dfrac{1}{\sqrt{3}}=\dfrac{24-h}{15} \\
 & \Rightarrow 15=\sqrt{3}\left( 24-h \right) \\
 & \Rightarrow 15=24\sqrt{3}-\sqrt{3}h \\
 & \Rightarrow \sqrt{3}h=24\sqrt{3}-15 \\
 & \Rightarrow h=\dfrac{24\sqrt{3}-15}{\sqrt{3}} \\
\end{align}$
Now we will substitute the value of $\sqrt{3}$ = 1.732. This result into
$\begin{align}
  & h=\dfrac{24\left( 1.732 \right)-15}{\left( 1.732 \right)} \\
 & \Rightarrow h=\dfrac{41.568-15}{1.732} \\
 & \Rightarrow h=\dfrac{26.568}{1.732} \\
 & \Rightarrow h=15.339 \\
\end{align}$
Hence, the height of EC is given by h = 15.339 metres approximately.

Note: If the value of $\sqrt{3}$ is not given to us then, we can also leave the value of height as $h=\dfrac{24\sqrt{3}-15}{\sqrt{3}}$. The diagram should be according to the statements of the question. Drawing the diagram stepwise will result in the right answer. Don’t get confused between the values of $\tan \left( {{30}^{\text{o}}} \right)$ and $\tan \left( {{60}^{\text{o}}} \right)$. The value of $\tan \left( {{30}^{\text{o}}} \right)=\dfrac{1}{\sqrt{3}}$ and $\tan \left( {{60}^{\text{o}}} \right)=\sqrt{3}$. We can also use the formula $\sin \left( \alpha \right)=\dfrac{perpendicular}{hypotenuse}$ and $\cos \left( \alpha \right)=\dfrac{base}{hypotenuse}$. For that we will use the Pythagoras theorem as well and solve as usual by substituting the required values into the formula. Focusing on these points we will get the right answer.