Question

The height of the image formed by a converging lens on a screen is $8cm$. For the same position of the object and screen again an image of size $12.5cm$ is formed on the screen by shifting the lens. The height of the object:
A) $\dfrac{{625}}{{32}}cm$
B) $\dfrac{{64}}{{12.5}}cm$
C) $10cm$
D) None

Answer 1

Hint: The two provided cases are obtained by having a normal step up and then by shifting the positions of the lens. Obtain mathematical expressions for both the cases using the magnification formula and lens formula. Then solve them together by value substitution of one into the other, using their relation to get the required answer.

Formula used:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
${M_1} = \dfrac{{{h_1}}}{h} = \dfrac{v}{u}$
${M_2} = \dfrac{{{h_2}}}{h} = \dfrac{{v'}}{{u'}}$

Complete solution:
As we know there are no changes in the position of the object or the screen in this question, and the only displacement is occurring for the position of the lens.
This question can be easily understood with the idea of a magnifying glass, let me explain it to you. Suppose you are trying to read a book with extremely small letters that you can only do with the help of a magnifying glass. Now you use a magnifying glass to view the letters, as we know similar to the question asked, a magnifying glass too has a converging lens, which is a convex lens. Now to get a better vision of the text we move the glass, keeping our eyes and the book in the same place.
We can make a diagram of the situation, and then do the basic math to arrive at the answer.

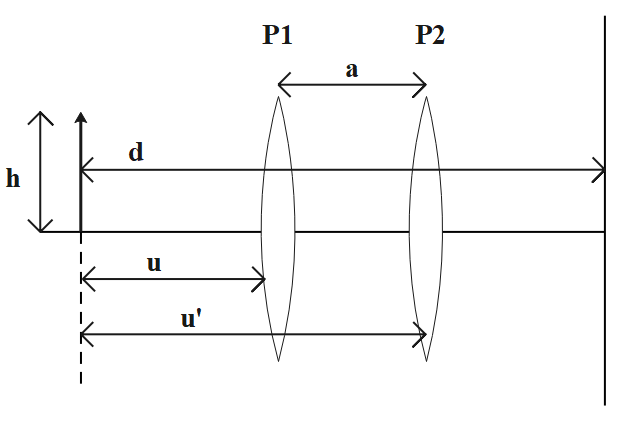
In the figure P1 is the first position and P2 is the second position. D is the distance between the object and the screen and h denotes the height of the object.
From lens formulae
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{{d - u}} - \dfrac{1}{u}$
Let ${h_1}$and ${h_2}$be the two image heights.
Magnification of first position can be written as
${M_1} = \dfrac{{{h_1}}}{h} = \dfrac{v}{u}$
And for second position
${M_2} = \dfrac{{{h_2}}}{h} = \dfrac{{v'}}{{u'}}$
Multiplying both equations and simplifying
${M_1}{M_2} = \dfrac{{{h_1}}}{h}\dfrac{{{h_2}}}{h} = \dfrac{v}{u}\dfrac{{v'}}{{u'}}$
On simplifying equations of image distance, we get
$\eqalign{
& v = u \cr
& v' = u' \cr} $
Therefore
${h_1}{h_2} = {h^2}$
Substituting the values
$\therefore h = \sqrt {8 \times 12.5} = 10cm$
Hence, the height of the object is $10cm$.

Therefore, option C is the correct answer.

Note:
Note that the above formula is independent of the distance between the two lenses, the effect is already included in the heights of the images. It is very important to use proper sign convention in solving this problem; otherwise it will lead to false results.