Question

The height of the cylinder of max, the volume that can be inscribed in a sphere of radius α is
1) \[\dfrac{{2\alpha }}{{\sqrt 3 }}\]
2) \[\dfrac{\alpha }{{\sqrt 2 }}\]
3) \[\dfrac{{5\alpha }}{4}\]
4) None of these.

Answer 1

Hint: We will first draw a diagram to visualize the question.

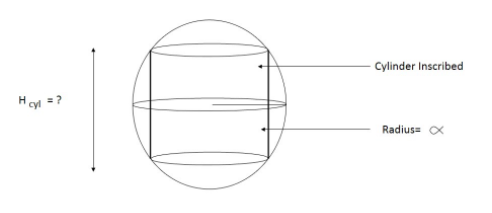
Now that we have a diagram, we will first write the volume of the cylinder in terms of \[{h_{cyl}}\] and α. We will then differentiate that formula and find the relation between \[{h_{cyl}}\] and α for the maximum volume.

Complete step by step solution: Given a cylinder of radius r and height \[{h_{cyl}}\], its volume is \[\pi {r^2}h\]
Now let’s pay closer attention to the diagram.

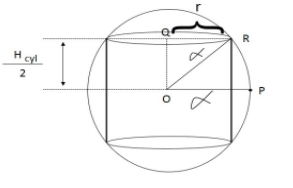
Looking at ∆OQR,
\[{r^2} + {\left( {\dfrac{{{h_{cyl}}}}{2}} \right)^2} = {\alpha ^2}\] (Pythagoras theorem)
So rearranging terms, we get.
     \[{r^2} = {\alpha ^2} - \dfrac{{h_{cyl}^2}}{4}\]
We want to substitute this value into the general volume of a cylinder.
     \[V = \pi {r^2}h_{cyl}^2 = \pi \left( {{\alpha ^2} - \dfrac{{h_{cyl}^2}}{4}} \right){h_{cyl}}\]
Now that we have V in term of α and \[{h_{cyl}}\], all we have to do is find \[\dfrac{{dV}}{{d{h_{cyl}}}}\] and set it to 0.
     \[\begin{gathered}
  \dfrac{{dV}}{{d{h_{cyl}}}} = \dfrac{d}{{d{h_{cyl}}}}\left( {\pi {\alpha ^2}{h_{cyl}} - \dfrac{\pi }{4}h_{cyl}^3} \right) \\
   = \pi {\alpha ^2} - \dfrac{{3\pi }}{4}h_{cyl}^2 = 0 \\
\end{gathered} \]
Rearranging, we get \[\dfrac{3}{4}h_{cyl}^2 = {\alpha ^2}\]
     \[h_{cyl}^2 = \dfrac{4}{3}{\alpha ^2}\]
     \[\therefore \boxed{{h_{cyl}} = \dfrac{2}{{\sqrt 3 }}\alpha }\]
It’s important at this stage to check the double derivative of volume, \[\dfrac{{{d^2}V}}{{dh_{cyl}^2}}\], first to make sure the value of \[{h_{cyl}}\] is indeed the maxima.
     \[\dfrac{{{d^2}V}}{{dh_{cyl}^2}} = \dfrac{d}{{d{h_{cyl}}}}\left( {\pi {\alpha ^2} - \dfrac{{3\pi }}{4}h_{cyl}^2} \right)\]
     \[ = - \dfrac{{6\pi }}{4}{h_{cyl}}\]. We know \[{h_{cyl}} > 0\] so this double derivative is NEGATIVE. Hence, our assumption was right and \[{h_{cyl}} = \dfrac{2}{{\sqrt 3 }}\alpha \] is a maxima.

Hence option A is correct.

Note: It is important to know WHY the double derivative being negative means we are dealing with a maximum.
     The double derivative of any quantity with respect to another refers to the rate of change of slope.
     A positive value means that as time goes on, slope keeps increasing. A negative value means that as time goes on, slope keeps decreasing on either side because it represents the highest point in the graph. Hence the double derivative has to be negative, indicating decreasing slopes.