Question

The height and the slant height of a cone are 21 cm and 28 cm, respectively. Find the volume of the cone.

Answer 1

Hint- In order to solve the problem we will use the formula of the volume of the cone in terms of height and the radius of the cone. Since in the problem, the radius of the cone is not mentioned so we will first use the Pythagoras theorem to find the radius of the cone.

Complete step-by-step answer:

In order to solve this problem, we will use the following figure:

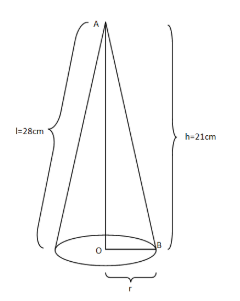
Given that:
Slant height of the cone = l =28 cm
Height of the cone = h = 28 cm
Let the radius of the cone = r cm
As we know that triangle AOB in the cone is right angled so let us use Pythagoras theorem in order to find the radius of the cone:
In right angled $\Delta AOB$
\[AO = 21cm,OB = \left( r \right)cm\& BA = 28cm\]
Let us use Pythagoras theorem for right angled triangle AOB.
According to Pythagoras theorem, for right angled triangle:
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Sid}}{{\text{e}}_1}} \right)^2} + {\left( {{\text{Sid}}{{\text{e}}_2}} \right)^2}$
Using the same for the given triangle AOB we get:
$ \Rightarrow {\left( {AB} \right)^2} = {\left( {AO} \right)^2} + {\left( {OB} \right)^2}$
Substituting the value in the equation we get:
$
   \Rightarrow {\left( l \right)^2} = {\left( h \right)^2} + {\left( r \right)^2} \\
   \Rightarrow {\left( {28} \right)^2} = {\left( {21} \right)^2} + {\left( r \right)^2} \\
   \Rightarrow {\left( r \right)^2} = {\left( {28} \right)^2} - {\left( {21} \right)^2} \\
   \Rightarrow {\left( r \right)^2} = \left( {28 + 21} \right)\left( {28 - 21} \right){\text{ }}\left[ {\because {{\left( x \right)}^2} - {{\left( y \right)}^2} = \left( {x + y} \right)\left( {x - y} \right)} \right] \\
   \Rightarrow {\left( r \right)^2} = \left( {49} \right)\left( 7 \right) \\
   \Rightarrow r = \sqrt {49 \times 7} \\
   \Rightarrow r = 7\sqrt 7 cm \\
 $
Now as we have the radius of the cone, we can easily find the volume of the cone.
As we know that volume of the cone is $\dfrac{1}{3}\pi {r^2}h$
So let us find the volume of the cone.
Volume:
$
   = \dfrac{1}{3}\pi {r^2}h \\
   = \left( {\dfrac{1}{3}\pi {{\left( {7\sqrt 7 } \right)}^2}21} \right)c{m^3} \\
 $
Now, let us simplify the term:
$
   = \left( {\dfrac{1}{3} \times \dfrac{{22}}{7} \times 7\sqrt 7 \times 7\sqrt 7 \times 21} \right)c{m^3} \\
   = \left( {\dfrac{1}{3} \times \dfrac{{22}}{7} \times 7 \times 7 \times 7 \times 21} \right)c{m^3} \\
   = \left( {22 \times 7 \times 7 \times 7} \right)c{m^3} \\
   = 7546c{m^3} \\
 $
Hence, the volume of the cone is $7546c{m^3}$ .

Note- This problem can also be solved by using the formula of volume of cone in terms of height and slant height. But that formula is a bit hard to remember and is not randomly used, so the method used here is the easiest one. Students must take extra care of units and must remember the Pythagoras theorem as it is commonly used in different types of problems.