Question

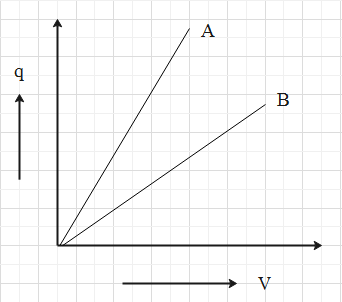
The given graph shows variation of charge versus potential difference V for two capacitors \[{{C}_{1}}\] and \[{{C}_{2}}\]. Both the capacitors have the same plate separation but plate area of \[{{C}_{2}}\], is greater than that of \[{{C}_{1}}\]. Which line (A or B) corresponds to \[{{C}_{1}}\] and \[{{C}_{2}}\] why?

Answer 1

Hint: The problem is based on the concept of the capacitance of the capacitor. Using the formula for calculating the capacitance of the capacitor, and finding the relation between the capacitance and the area of the capacitor, this problem can be easily solved.
Formula used:
\[C=\dfrac{{{\varepsilon }_{0}}A}{d}\]

Complete answer:
The capacitance of a capacitor is derived as follows.
The capacitance of a capacitor is directly proportional to the area of the parallel plates of a capacitor.
So, we have,
\[C\propto A\] …… (1)
The capacitance of a capacitor is inversely proportional to the separation between the parallel plates of a capacitor.
So, we have,
\[C\propto \dfrac{1}{d}\]
Combine both the equations.
\[C\propto \dfrac{A}{d}\]
Thus, the capacitance of a capacitor is given by the formula as below.
\[C=\dfrac{{{\varepsilon }_{0}}A}{d}\]
Where C is the capacitance, \[{{\varepsilon }_{0}}\] is the permittivity of dielectric, A is the cross-sectional area of the plates and d is the separation between the plates.
Now consider the separate equations for the two capacitors \[{{C}_{1}}\] and \[{{C}_{2}}\].
We have,
\[\begin{align}
  & {{C}_{1}}=\dfrac{{{\varepsilon }_{0}}{{A}_{1}}}{{{d}_{1}}} \\
 & {{C}_{2}}=\dfrac{{{\varepsilon }_{0}}{{A}_{2}}}{{{d}_{2}}} \\
\end{align}\]

From given question, we can derive two statements, those are,
Both the capacitors have the same plate separation.
\[\begin{align}
  & {{C}_{1}}=\dfrac{{{\varepsilon }_{0}}{{A}_{1}}}{d} \\
 & {{C}_{2}}=\dfrac{{{\varepsilon }_{0}}{{A}_{2}}}{d} \\
\end{align}\]

The plate area of \[{{C}_{2}}\], is greater than that of \[{{C}_{1}}\].
Let us assume that the plate area of \[{{C}_{2}}\], is double that of \[{{C}_{1}}\].
Now, we have the equation as.
\[\begin{align}
  & {{C}_{1}}=\dfrac{{{\varepsilon }_{0}}{{A}_{1}}}{d} \\
 & {{C}_{2}}=\dfrac{{{\varepsilon }_{0}}2{{A}_{1}}}{d} \\
\end{align}\]
Solving the above equations, we get,
\[{{C}_{2}}=2{{C}_{1}}\] …… (2)

Considering the equations (1) and (2), we can say that the capacitor with the greater area will have the greater capacitance, that is the slope.
As the slope of capacitor \[{{C}_{2}}\] is greater than that of capacitor \[{{C}_{1}}\], thus, the line A corresponds to capacitor \[{{C}_{2}}\] and line B corresponds to capacitor \[{{C}_{1}}\].

Note:
The things to be on your finger-tips for further information on solving these types of problems are: The problems involving the graph concepts can be easily solved by using the formulae that relate the parameters given in the graph.