Question

The four walls of the room are 6 m long 3 m broad and 3.5 metre height are to be painted. If the rate of painting is Rs. 650 per $ {m^2} $ square find the total cost of painting.

Answer 1

Hint: The room is cuboidal in shape and each wall is rectangular shape, we can find the total surface area that is to be painted. Multiplying this area with the given cost of per $ {m^2} $ , we will get the required cost of painting.
Area of rectangle = $ l \times b $ , where,
l and b are its length and breadth respectively.

Complete step by step solution:

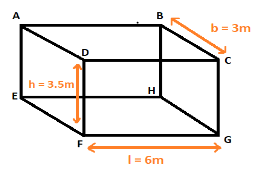
The room is in the shape of a cuboid and all the walls consisting of the room will be rectangular in shape. The wall of the rooms are given to be 6 m long 3 m broad and 3.5 metre height
The area of four walls to be painted in the drawn figure are:
 $ ar(ADEF) + ar(BCGH) + ar(DCGF) + ar(ABHE) $
The area of respective rectangles are given by the product of their respective lengths and breadths are:
 $
\Rightarrow A = \left( {b \times h} \right) + \left( {b \times h} \right) + \left( {l \times h} \right) + \left( {l \times h} \right) \\
\Rightarrow A = 2\left( {b \times h} \right) + 2\left( {l \times h} \right) \\
\Rightarrow A = 2h\left( {l + b} \right) \;
  $
The given dimensions of the room are:
Length (l) = 6 m
Breadth (b) = 3 m
Height (h) = 3.5 m
Substituting these values, we get:
 $
\Rightarrow A = \left[ {2 \times 3.5\left( {6 + 3} \right)} \right]{m^2} \\
\Rightarrow A = \left[ {2 \times 3.5 \times 9} \right]{m^2} \\
\Rightarrow A = 63\;{m^2} \;
  $
Thus, the required area to be painted is $ 63\;{m^2} $ .
Now, it is given that the cost of painting $ 1\;{m^2} $ is Rs. 650, then the cost of painting for $ 63\;{m^2} $ can be calculated using the unitary method as:
 $
  1\;{m^2} = Rs.650 \\
  63\;{m^2} = \dfrac{{Rs.650}}{1} \times 63 \\
   \Rightarrow Rs.40950 \;
  $
Therefore, the total cost of painting the four walls of the room is Rs. 40950
So, the correct answer is “Rs. 40950”.

Note: As the area of the four faces of the cuboid was to be calculated, we could have directly use the formula for its curved surface or lateral surface given as:
 $ 2h\left( {l + b} \right) $
The cost of painting was given for per $ {m^2} $ which means for every unit area of $ 1\;{m^2} $ , for finding the cost for the required area, the area can be multiplied directly with the given cost without the use of unitary method. But it is always better to use a unitary method so as to reduce the chance of making mistakes.