Question

The formula used for surface area of a cone is (s denotes slant height):
A . $\pi r\left( r+s \right)sq.units$
B . $\pi r\left( 2r+s \right)sq.units$
C . $2\pi r\left( r+s \right)sq.units$
D . $\pi r{{\left( r+s \right)}^{2}}sq.units$

Answer 1

Hint: To solve this question, we will first find out the curved surface area of the cone. The curved surface area of the cone will be obtained by cutting open the cone and rolling it out. We will find out that the shape will be the sector of a circle. The area of this sector will be equal to the curved surface area of the cone. The flat surface area of the cone will be equal to the area of the circular base, and then we will obtain the total surface area of the cone by adding curved surface area and flat surface area of the cone.

Complete step-by-step answer:
Before finding out the total surface area of a cone, we should know what a cone is. A cone is a three dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex. Now, first we will determine the curved surface area:

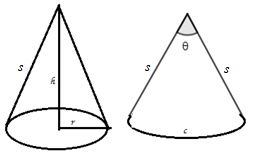
To find out the curved surface area, we will cut open the cone, like can see that the shape obtained is a sector of a circle with radius equal to the slant height and length of arc equal to the circumference of the circular base. The area of the sector with radius $\pi $ and angle between the radiuses as $\theta $ is given by the formula.
Area of sector $=\dfrac{\theta }{2\pi }\times \pi {{r}^{2}}$
Thus, we have:
Area of sector $=\dfrac{\theta }{2\pi }\times \pi {{\left( s \right)}^{2}}$ ……………….. (1)
Now, in our case, $\theta =\dfrac{\text{circumference of circle}}{\text{radius of circle}}$ .
$\Rightarrow \theta =\dfrac{\pi r}{s}$ ………… (2)
Now, we will substitute the value of $\theta $ from equation (2) to equation (1). Thus, we have:
CSA = Area of sector $=\dfrac{\left( \dfrac{2\pi r}{s} \right)}{2\pi }\times \pi {{s}^{2}}$
Curved surface area $=\dfrac{2\pi r}{2\pi s}\times \pi {{s}^{2}}$
Curved surface area $=\pi rs$ ……………………. (3)
Now, we will calculate the area of the flat circular surface. The area of circle is given by:
Area of circle $=\pi {{r}^{2}}$
Therefore, flat surface area $=\pi {{r}^{2}}$ ………………………. (4)
Now, we will find the total surface area of the cone. The total surface area of the cone is equal to the area of curved surface plus area of flat surface. Thus,
\[\text{Total surface area = Curved surface area + Flat surface area}\]
$\begin{align}
  & =\pi rs+\pi {{r}^{2}} \\
 & =\pi r\left( s+r \right)sq.units \\
\end{align}$
Hence, option A is correct.

Note: While doing the calculations, we have assumed that the cone is a right circular cone, this means that the axis of the cone is the line meeting the open to the midpoint of the circular base. Also, if a cone is not the right circular cone, then the slant height of the cone will vary and not remain constant.