
The following table gives the distribution of students of two sections according to the marks obtained by them:
Represent the marks of the students of both the sections on the same graph of two frequency polygons. From the two polygons compare the performance of two sections.
Marks Section A FrequencySection A MarksSection B FrequencySection B $0 - 10$ $3$ $0 - 10$ $5$ $10 - 20$ $9$ $10 - 20$ $19$ $20 - 30$ $17$ $20 - 30$ $15$ $30 - 40$ $12$ $30 - 40$ $10$ $40 - 50$ $9$ $40 - 50$ $1$
| Marks Section A | FrequencySection A | MarksSection B | FrequencySection B |
| $0 - 10$ | $3$ | $0 - 10$ | $5$ |
| $10 - 20$ | $9$ | $10 - 20$ | $19$ |
| $20 - 30$ | $17$ | $20 - 30$ | $15$ |
| $30 - 40$ | $12$ | $30 - 40$ | $10$ |
| $40 - 50$ | $9$ | $40 - 50$ | $1$ |
Answer
534k+ views
Hint: In this question we are asked to represent the frequency polygons on the same graph. In order to proceed with this question we need to know what frequency polygons are. A frequency polygon is the graphical representation. It is similar to histogram. It is used to compare sets of data which are of similar nature. It uses a line graph to represent required quantitative data. Class marks are calculated by dividing the sum of upper and lower limit of class interval by $2$.
Complete step by step solution:
We’ll calculate class marks first,
$class\;marks = \dfrac{{upper{\text{ }}limit{\text{ }} + {\text{ }}lower{\text{ }}limit}}{2}$
For example - $class\;marks(0 - 10) = \dfrac{{0 + 10}}{2} = 5$
Now we’ll plot it on line graph,
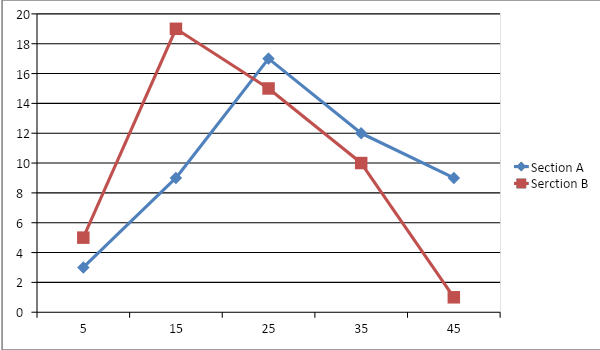
After comparing – When we look at the line graph above, we can observe that Section A is right of Section B which means, more students in Section A have higher marks than students in Section B. It implies performance of Section A is better than B.
Note: The main objective to represent the information in graphical representation is to convert it into a form which can be easily interpreted. And also, plotting information of same type makes it easy to compare both the information. When we are given class intervals it is compulsory to calculate class marks.
Complete step by step solution:
We’ll calculate class marks first,
$class\;marks = \dfrac{{upper{\text{ }}limit{\text{ }} + {\text{ }}lower{\text{ }}limit}}{2}$
For example - $class\;marks(0 - 10) = \dfrac{{0 + 10}}{2} = 5$
| Marks | Class marksSection A | FrequencySection A | Marks | Class marksSection B | FrequencySection B |
| $0 - 10$ | 5 | $3$ | $0 - 10$ | 5 | $5$ |
| $10 - 20$ | 15 | $9$ | $10 - 20$ | 15 | $19$ |
| $20 - 30$ | 25 | $17$ | $20 - 30$ | 25 | $15$ |
| $30 - 40$ | 35 | $12$ | $30 - 40$ | 35 | $10$ |
| $40 - 50$ | 45 | $9$ | $40 - 50$ | 45 | $1$ |
Now we’ll plot it on line graph,

After comparing – When we look at the line graph above, we can observe that Section A is right of Section B which means, more students in Section A have higher marks than students in Section B. It implies performance of Section A is better than B.
Note: The main objective to represent the information in graphical representation is to convert it into a form which can be easily interpreted. And also, plotting information of same type makes it easy to compare both the information. When we are given class intervals it is compulsory to calculate class marks.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




