Question

The focal length of a plano convex lens is $'f'$ and its refractive index is $1.5$. It is kept over a plane glass plate with its curved surface touching the glass plate. The gap between the lens and the glass plate is filled by a liquid. As a result, the effective focal length of the combination becomes $2f$. Then the refractive index of the liquid is
A. $1.25$
B. $1.33$
C. $1.5$
D. $2$

Answer 1

Hint: We can solve this question with help of lens maker formulas. Lens is the piece of transparent material that has two curved surfaces . There are many types of lenses such as plano convex, convex, concave, plano concave etc. The formula which is used for calculation of focal length is $\dfrac{1}{F} = \dfrac{1}{V} + \dfrac{1}{u}$
Where $F,V,u$ is focal length of lens, distance of image from the lens and distance of object from the lens respectively.

Complete step by step answer:
If we combine the two lenses of different or same focal length , a new combination of lens is formed and its focal length can be calculated with the lens maker formula . The focal length of a lens depends upon the refractive index of the lens and the radius of its curvatures. Lens maker formula is written as follows:
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ , where $f$ is the focal length of the combination, $\mu $ is refractive index of lens and ${R_1},{R_2}$ is the radius of curved surfaces respectively.

For the given question figure is as follows :

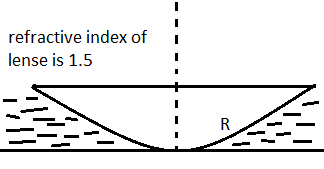
From the lens maker formula, focal length of plano convex lens is $\dfrac{1}{f} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{{ - \infty }} - \dfrac{1}{{ - R}}} \right)$
For the plan surface of the lens if ${R_1} = - \infty $, and curved surface ${R_2} = - R$.
So,
$
  \dfrac{1}{f} = \dfrac{1}{{2R}} \\
   \Rightarrow f = 2R \\
$

Now, we can assume the fluid below the combination lens as a plano concave lens of refractive index of $\mu $ and focal length of $f'$ . So,
$\dfrac{1}{{f'}} = \dfrac{{1 - \mu }}{R}$
For new combination focal length is, $\dfrac{1}{F} = \dfrac{1}{{f'}} + \dfrac{1}{f}$, focal length for this lense is given in question i.e. $2f$.

$\dfrac{1}{{2f}} = \dfrac{1}{f} + \dfrac{{1 - \mu }}{R} \Rightarrow \dfrac{{1 - \mu }}{R} = \dfrac{{ - 1}}{{2f}} = \dfrac{{ - 1}}{{4R}}$
$
   \Rightarrow 1 - \mu = 0.25 \\
   \Rightarrow \mu = 1.25 \\
$

Then the refractive index of the liquid is 1.25. Option A is the correct answer of the given question.

So, the correct answer is “Option A”.

Note:
The lenses are used in different optical instruments such as telescope, microscopes . These instruments are made up of different combinations of different focal lengths. We use lens maker formulas for the manufacturing lenses of the desired focal length.