Question

The figure shows Young’s double-slit experiment setup. It is observed that when a thin transparent sheet of thickness $t$ and refractive index $\mu $ is put in front of one of the slits, the central maximum gets shifted by a distance equal to $n$ fringe widths. If the wavelength of the light used is $\lambda $, t will be

A. $\dfrac{2D\lambda }{a(\mu -1)}$
B. \[\dfrac{D\lambda }{a(\mu -1)}\]
C. $\dfrac{2nD\lambda }{a(\mu -1)}$
D. $\dfrac{nD\lambda }{a(\mu -1)}$
E. No answer

Answer 1

Hint: In young’s double-slit experiment is an experiment where a single monochromatic beam of the slit is passed through the two slits. By the wave nature of the light, it is explained that by the overlapping of the waves of the two diffracted lights the dark and bright alternative fringe pattern can be observed on the screen placed at a distance D from the slit.

Complete step by step answer:
The young’s double slit setup with a sheet introduced of a thickness t can be shown by the following diagram,

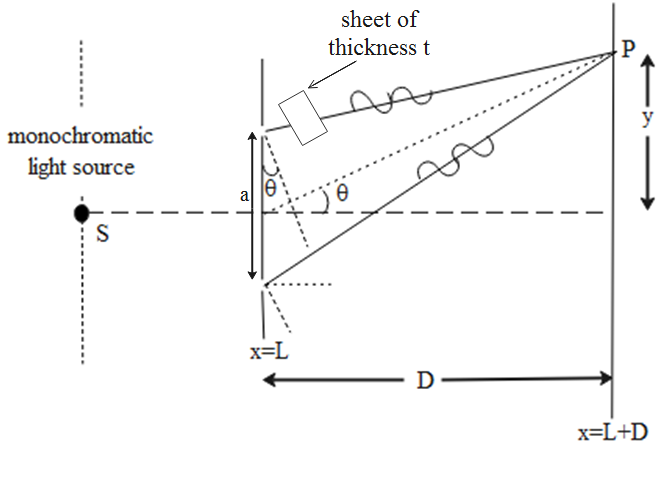
When a sheet is introduced near one of the openings it is found that all the fringes shift by a certain distance. This shift is known as the path difference.
The fringe with before the occurrence of the path difference is given by,
$\beta =\dfrac{D\lambda }{a}$
Where,
$D$ Is the distance between the openings and the screen
\[a\] Is the distance between the two slits
$\lambda $ Is the wavelength of the light beam
The path difference is given by,
$d\sin \theta =\left( \mu -1 \right)t$
Where,
$\mu $ Is the refractive index
$t$ Is the thickness of the sheet
The new fringe width of the n fringes is given as
$\left( \mu -1 \right)t\dfrac{D}{d}=n\dfrac{D\lambda }{d}$
So by simplifying the above equation,
$\begin{align}
  & \left( \mu -1 \right)t=n\lambda \\
 & \Rightarrow t=\dfrac{n\lambda }{\left( \mu -1 \right)} \\
\end{align}$
So the thickness of the sheet which is placed in the front of one of the slits or opening is given as $\left( \dfrac{n\lambda }{\left( \mu -1 \right)} \right)$.
So when we give a glance over the mentioned options we found that no option from A, B, C, D satisfies the value of the thickness of the sheet.
Thus the correct option which satisfies the question is Option E.

Note: The external sheet of thickness $t$ introduced in the path of the light beam from one of the optics provides an extra refractive medium in the young’s double-slit setup. The refraction occurs due to the change in the speed of the while passing through the sheet. This refraction results in the change in the path of the light and a shift in the fringe pattern obtained on the screen.