Question

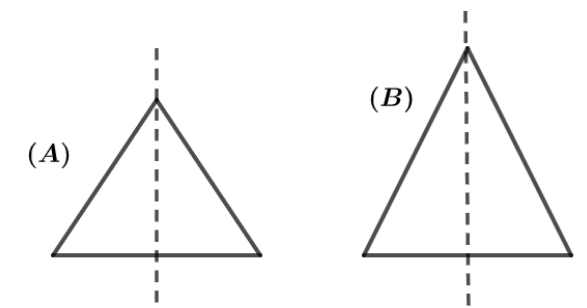
The figure shows two cones A and B with the conditions ${h_A} < {h_B}$ , ${\rho _A} > {\rho _B}$ , ${R_A} = {R_B}$ and ${m_A} = {m_B}$. Identify the correct statement about their axes of symmetry.

A. Both have same moment of inertia
B. $A$ has greater moment of inertia
C. $B$ has greater moment of inertia
D. Nothing can be said

Answer 1

Hint: In physics, Moment of inertia of a body is defined as the tendency of a body to oppose or to resist the angular acceleration produced in the body due to rotational motion. Moment of inertia is a scalar quantity and its general mathematical formula can be written as $I = m{r^2}$ where $m$ is the mass of the body and $r$ is the perpendicular distance between the body and the axis of rotation.

Complete step by step answer:
As we know that, the general formula for the moment of inertia for a solid cone about the axes of symmetry of the cone having a mass of $M$ and radius of circular base $R$ is given by $I = \dfrac{3}{{10}}M{R^2}$ . We can see that the moment of inertia of a solid cone about the axes of symmetry is independent of its height. So, according to the given conditions for cones $A$ and $B$ we have, ${h_A} < {h_B}$ which will have no effect on the magnitude of moment of inertia of both cones.

And we have, the radii of both cones A and B are related as ${R_A} = {R_B}$ and their masses are related as ${m_A} = {m_B}$. So,
Moment of inertia of cone $A$ will be ${I_A} = \dfrac{3}{{10}}{m_A}{R_A}^2$
Moment of inertia of cone $B$ will be ${I_B} = \dfrac{3}{{10}}{m_B}{R_B}^2$
Since we have, ${R_A} = {R_B}$ and ${m_A} = {m_B}$ so, we can say that ${I_A} = {I_B}$
So, both cones $A$ and $B$ will have the same moment of inertia.

Hence, the correct option is A.

Note: It should be remembered that, Moment of inertia is independent of the height of the cone. The SI unit of moment of inertia is $kg{m^2}$ and since moment of inertia is the capacity to oppose angular acceleration in it, the mathematical formula between moment of inertia and angular acceleration is written as $\vec \tau = I\vec \alpha $ where $\vec \tau $ is the torque acting on a body and $\vec \alpha $ is the angular acceleration produced in the body.