Question

The figure shows a potentiometer circuit. The length of potentiometer wire is L and its resistance is 4R. If the cell is ideal, select the correct option –

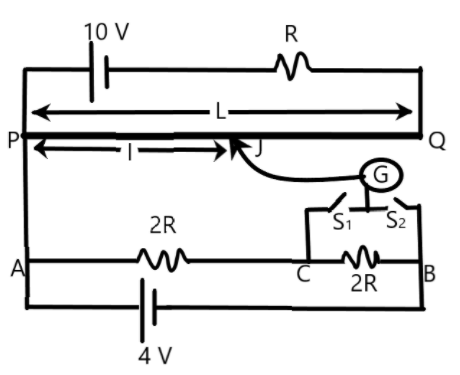
A) When only \[{{S}_{1}}\] is closed, \[\dfrac{l}{L}=\dfrac{1}{4}\]
B) When only \[{{S}_{2}}\] is closed \[\dfrac{l}{L}=\dfrac{1}{2}\]
C) When \[{{S}_{1}}\] and \[{{S}_{2}}\] are closed \[\dfrac{l}{L}=\dfrac{1}{4}\]
D) When \[{{S}_{1}}\] and \[{{S}_{2}}\]are closed \[\dfrac{l}{L}=\dfrac{1}{2}\]

Answer 1

Hint: We need to relate the resistance of the potentiometer wire, its length and the resistance in the circuits to find the emf dependence of the balancing length in the given problem. The ratio is the emf of the cell and the source voltage which drives the device.

Complete answer:
We are given a potentiometer setup with an ideal cell connected to it. We can easily find the ratio emf from the ideal cell and the source at different situations by properly identifying the circuit.
Let us find the potential drop per unit length for the potentiometer wire PQ of length ‘L’. The total resistance of the circuit when both the switches \[{{\text{S}}_{\text{1}}}\text{ and }{{\text{S}}_{\text{2}}}\] are open is 5R. Using this information, we can find the current through the element PQ in this situation as –
\[\begin{align}
  & V=IR \\
 & \Rightarrow 10V=I(5R) \\
 & \Rightarrow I=\dfrac{2}{R} \\
\end{align}\]

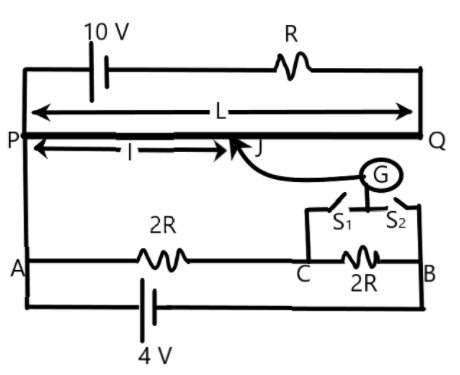
Now, the potential drop across PQ when both the switches are open is –
\[\begin{align}
  & {{V}_{PQ}}=IR \\
 & \Rightarrow {{V}_{PQ}}=\dfrac{2}{R}(4R) \\
 & \Rightarrow {{V}_{PQ}}=8V \\
\end{align}\]
Now, we know the voltage drop across the length ‘L’ in the initial condition as 8V.
The potential drop of the potentiometer wire per unit length can be given as –
\[\begin{align}
  & \phi =\dfrac{{{V}_{PQ}}}{L} \\
 & \Rightarrow \phi =\dfrac{8}{L}V{{m}^{-1}} \\
\end{align}\]
When we consider the circuit along the resistors in AB with the emf of 4V. Each of the resistors has a potential drop of 2V each across them.
When the switch \[{{\text{S}}_{\text{1}}}\]is closed, the balancing length l is attained with the potential drop of 2V along PJ.
i.e.,
\[{{V}_{PJ}}=2V\]
The ratio of the balancing lengths in this situation is given as –
\[\begin{align}
  & \Rightarrow \dfrac{l}{L}=\dfrac{{{V}_{PJ}}}{{{V}_{PQ}}} \\
 & \therefore \dfrac{l}{L}=\dfrac{2}{8}=\dfrac{1}{4} \\
\end{align}\]
Now, when the switch \[{{S}_{2}}\]is closed the voltage drop across PJ to attain the balancing length l is
\[{{V}_{PJ}}=4V\]
So, the ratio of balancing lengths can be given as –
\[\begin{align}
  & \Rightarrow \dfrac{l}{L}=\dfrac{{{V}_{PJ}}}{{{V}_{PQ}}} \\
 & \therefore \dfrac{l}{L}=\dfrac{4}{8}=\dfrac{1}{2} \\
\end{align}\]
From the above two results we can conclude that the ratio of balancing lengths are different when the two switches are closed.

The correct answers are option A and B.

Note:
The voltage across only one resistor is to be considered for the first case when the first switch is closed, in the second case, both the resistors become part of the circuit, so both have to be considered. Thus the factor of the ratio becomes double.