Question

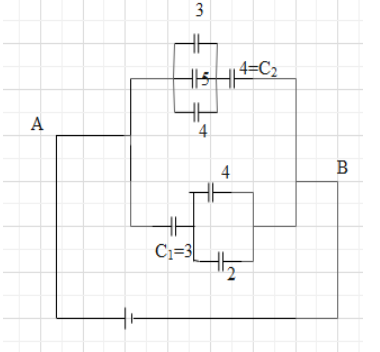
The figure shows a network of seven capacitors. If the charge on the 5μF capacitor is 10μC, the potential difference between the points A and C is given as \[\dfrac{x}{3}\].

Answer 1

Hint: We should have knowledge about kirchhoff's law of capacitance for solving this circuit. Q=CV, we will deal with equivalent capacitance across two points. Charge conservation method should be kept in mind. We will find \[{{Q}_{eq}}\], \[{{C}_{eq}}\] and ${{V}_{AB}}$ and by using formula we will solve the question.

Formula used:
\[{{Q}_{eq}}={{C}_{eq}}{{V}_{AB}}\]

Complete answer:

Firstly we will find potential across 5 capacitor
Let the potential across the \[5\mu f\] capacitor be \[{{v}_{5}}\].
Potential across \[5\mu f\] is \[{{v}_{5}}=\dfrac{{{q}_{5}}}{{{c}_{5}}}\]
\[=\dfrac{10}{5}=2\]
As we can see that\[\left( 3\mu f,4\mu f,5\mu f \right)\] are in parallel in below given diagram

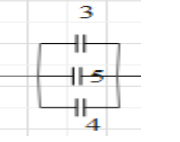
So now we will find charge on \[3\mu f\] and \[4\mu f\] capacitor voltage across both the capacitance will be the same as both are in parallel i.e =2volts.
Charge on \[3\mu f\] is \[{{Q}_{3}}=3\times 2=6\mu C\]
Charge on \[4\mu f\] is \[{{Q}_{4}}4\times 2=8\mu C\]
Charge on \[5\mu f\] is \[{{Q}_{5}}=5\times 2=10\mu C\]
Now we can see that \[{{C}_{2}}\] is in series with \[\left( 3\mu f,4\mu f,5\mu f \right)\]so charge on \[{{C}_{2}}\] and group \[\left( 3\mu f,4\mu f,5\mu f \right)\]are same.
So we can find the charge on \[{{C}_{2}}\] is \[{{Q}_{2}}=10+6+8=24\mu C\]
And potential across it \[{{V}_{2}}=\dfrac{24}{4}=6V\]
Thus we will now find potential across point A and B
\[{{V}_{AB}}={{V}_{5}}+{{V}_{2}}=2+6=8V\]
Now equivalent capacitance of lower branch of circuit is
\[{{C}_{eq}}=\dfrac{3\left( 4+2 \right)}{3+4+2}=2\mu f\] And;
Total equivalent charge\[{{Q}_{eq}}={{C}_{eq}}{{V}_{AB}}=2\left( 8 \right)=16\mu C\]
\[\therefore {{V}_{AC}}=\dfrac{{{Q}_{eq}}}{3}=\dfrac{16}{3}\]
Thus on comparing it with \[\dfrac{x}{3}\] we obtain x=16.
On solving the circuit by basic charge conservation method we obtain that x=16.

Note:
We have to apply charge conservation carefully properties of capacitor in series and parallel should be kept in mind
Formula to find the charge on capacitor is
q=CV
Where,
q=charge on capacitor
V= voltage applied across capacitor
C= Capacitance of capacitor
When voltage is applied across a parallel plate capacitor it produces positive charge on one plate and negative charge on another plate. Charge across the capacitor is directly proportional to voltage.