Question

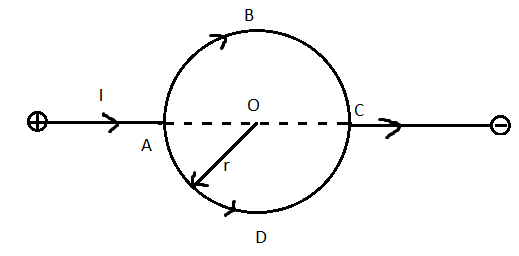
The figure shows a circular loop with radius $r$. The resistance of arc ABC is $5\Omega $ and that of ADC is $10\Omega $. Magnetic field at the center of the loop is:

A.)$\dfrac{{{\mu }_{0}}I}{3r}\otimes $
B.)$\dfrac{{{\mu }_{0}}I}{15r}\otimes $
C.)$\dfrac{{{\mu }_{0}}I}{12r}\odot $
D.)$\dfrac{{{\mu }_{0}}I}{6r}\odot $

Answer 1

Hint: This problem can be solved by using the expression for the magnetic field due to a semicircular current carrying coil at its center, separately for arcs ABC and ADC. Both of them will have different currents based on their resistances. The sum of these two magnetic fields keeping in mind their directions using the right hand thumb rule, will give the total magnetic field at the center.
Formula used:
The magnetic field due to a current carrying semicircular coil at its center is given by

$B=\dfrac{{{\mu }_{0}}I}{4R}$

Where $I$ is the current in the coil, $R$ is the radius of the coil and ${{\mu }_{0}}$ is the permeability of free space.
The direction of the magnetic field is given by the right hand thumb rule which states that if we curl the fingers of our right hand in the direction of the current along the coil, our thumb points towards the direction of the magnetic field at the center.

When a current $I$ splits into two branches, one with a resistance ${{R}_{1}}$ and another with resistance ${{R}_{2}}$, the respective currents ${{I}_{1}}$ and ${{I}_{2}}$ flowing through the two branches is given by,

${{I}_{1}}=\dfrac{{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}I$ and ${{I}_{2}}=\dfrac{{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}}I$

Complete step by step answer:
Here we are given a circular coil and a current I branches into the two halves of the coil. Essentially, the circle can be considered as two parallel semi circular branches.
We will find out the magnetic field at the center of the coil due to the respective currents flowing in each branch and sum them up in the end to get the total magnetic field at the center.
The magnetic field due to a current carrying semicircular coil at its center is given by

$B=\dfrac{{{\mu }_{0}}I}{4R}$ --(1)

Where $I$ is the current in the coil, $R$ is the radius of the coil and ${{\mu }_{0}}$ is the permeability of free space.
The direction of the magnetic field is given by the right hand thumb rule which states that if we curl the fingers of our right hand in the direction of the current along the coil, our thumb points towards the direction of the magnetic field at the center.

We will find out the currents flowing in each branch as a fraction of the total current by taking the resistance of each branch in consideration.
When a current $I$splits into two branches, one with a resistance ${{R}_{1}}$ and another with resistance${{R}_{2}}$, the respective currents ${{I}_{1}}$ and ${{I}_{2}}$ flowing through the two branches is given by,

${{I}_{1}}=\dfrac{{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}I$ and ${{I}_{2}}=\dfrac{{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}}I$ --(2)

Hence, now let us analyze the question.

Let the resistance of the arc ABC be ${{R}_{ABC}}$.
We are given that ${{R}_{ABC}}=5\Omega $.
Let the resistance of the arc ADC be ${{R}_{ADC}}$.
We are given that ${{R}_{ADC}}=10\Omega $.
The total current entering the circular coil is given as $I$.
The radius of the coil is $r$.

Let the currents flowing in branches ABC and ADC be ${{I}_{ABC}}$ and ${{I}_{ADC}}$ respectively.
Therefore, using equation (2), we get,

${{I}_{ABC}}=\dfrac{{{R}_{ADC}}}{{{R}_{ABC}}+{{R}_{ADC}}}I$
$\therefore {{I}_{ABC}}=\dfrac{10}{5+10}I=\dfrac{10}{15}I=\dfrac{2}{3}I$ ---(3)

Similarly, using (2), we get,

${{I}_{ADC}}=\dfrac{{{R}_{ABC}}}{{{R}_{ABC}}+{{R}_{ADC}}}I$
$\therefore {{I}_{ABC}}=\dfrac{5}{5+10}I=\dfrac{5}{15}I=\dfrac{1}{3}I$ --(4)

Let the magnetic field at the center of the coil due to the current flowing in arc ABC and arc ADC be ${{B}_{ABC}}$ and ${{B}_{ADC}}$respectively.
Plugging in the values and using equation (1), and using (3) and (4) we get,

${{B}_{ABC}}=\dfrac{{{\mu }_{0}}{{I}_{ABC}}}{4r}=\dfrac{1}{3}\dfrac{{{\mu }_{0}}I}{4r}$into the plane of the screen (using the right hand thumb rule)
$\therefore {{B}_{ABC}}=\dfrac{1}{3}\dfrac{{{\mu }_{0}}I}{4r}\otimes $ --(5)

where the symbol $\otimes $ means that the magnetic field points into the plane of the screen.
Similarly,

${{B}_{ADC}}=\dfrac{{{\mu }_{0}}{{I}_{ADC}}}{4r}=\dfrac{2}{3}\dfrac{{{\mu }_{0}}I}{4r}$out of the plane of the screen (using the right hand thumb rule)
${{B}_{ADC}}=\dfrac{2}{3}\dfrac{{{\mu }_{0}}I}{4r}\odot $ --(6)

where the symbol $\odot $ means that the magnetic field points out of the plane of the screen.

The total magnetic field at the center is the sum of that due to the two branches. Hence,
$B={{B}_{ABC}}+{{B}_{ADC}}$

where $B$ is the required magnetic field at the center of the coil.
Therefore using the values form (5) and (6), we get,

$B=\dfrac{1}{3}\dfrac{{{\mu }_{0}}I}{4r}\otimes +\dfrac{2}{3}\dfrac{{{\mu }_{0}}I}{4r}\odot $
$=-\dfrac{1}{3}\dfrac{{{\mu }_{0}}I}{4r}\odot +\dfrac{2}{3}\dfrac{{{\mu }_{0}}I}{4r}\odot =\dfrac{1}{3}\dfrac{{{\mu }_{0}}I}{4r}\odot =\dfrac{{{\mu }_{0}}I}{12r}\odot $ [For a vector $\overrightarrow{V}$ $\left( V\otimes =-V\odot \right)$ ]

Hence, the required magnetic field value at the center is $\dfrac{{{\mu }_{0}}I}{12r}\odot $.
Hence, the correct option is C) $\dfrac{{{\mu }_{0}}I}{12r}\odot $.

Note: Students often forget to take into account that the magnetic fields produced by the currents in the two branches are opposite in direction and cancel each other out to an extent. They simply add up the two magnitudes without taking into account the direction. This leads to a completely wrong answer. An easy way to remember the meaning of the symbols $\otimes $ and $\odot $ is to relate them to an arrow. The $\otimes $looks like the back of an arrow going away from you into the screen, and hence, the symbol $\otimes $ means that the direction of the vector is away from you into the plane of the screen.
Similarly, the $\odot $ like the front pointed end of an arrow coming towards you out of the screen, and hence, the symbol $\odot $means that the direction of the vector is towards you out of the plane of the screen.