Question

The figure below shows three cylindrical copper conductors along with their face areas and lengths. Compare the resistance and the resistivity of the three conductors. Justify your answer.
A.

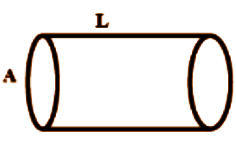
B.

C.

Answer 1

Hint: Electrical resistivity is the opposite of electrical conductivity. It is the measure of a material's ability to oppose the flow of current.

Formula used: We will use the following formula to solve this question
\[{\text{R}} = \rho \dfrac{L}{A}\]
Where
${\text{R}}$ is the resistance of the material
$\rho $ is the resistivity of the material
${\text{L}}$ is the length of the material
${\text{A}}$ is the cross sectional area of the material

Complete step by step answer:
For the figure (A.), we have been provided with the following information:
Length of the cylinder \[ = L\]
Cross sectional area of the cylinder \[ = A\]
Now we will simply put these values in the formula to find out resistance
So, we get
\[{R_A} = \rho \dfrac{L}{A}\]
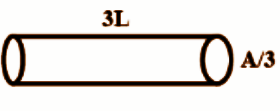
For the figure (B.), we have been provided with the following information:
Length of the cylinder \[ = 3L\]
Cross sectional area of the cylinder \[ = \dfrac{A}{3}\]
Now we will simply put these values in the formula to find out resistance
So, we get
\[{R_B} = \rho \dfrac{{3L}}{{\left( {\dfrac{A}{3}} \right)}}\]
We can rewrite this equation as
\[{R_B} = \rho \dfrac{{9L}}{A}\]
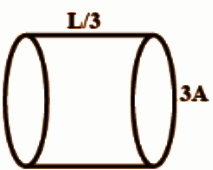
For the figure (C.), we have been provided with the following information:
Length of the cylinder \[ = \dfrac{L}{3}\]
Cross sectional area of the cylinder \[ = 3A\]
Now we will simply put these values in the formula to find out resistance
So, we get
\[{R_C} = \rho \dfrac{{\left( {\dfrac{L}{3}} \right)}}{{3A}}\]
We can rewrite this equation as
\[{R_C} = \dfrac{1}{9}\left( {\rho \dfrac{L}{A}} \right)\]
Comparing \[{R_A}\], \[{R_B}\], and \[{R_C}\], we can observe that
\[{R_B} = 9{R_A}\]
And
\[{R_C} = \dfrac{1}{9}{R_A}\]
Therefore, we can arrange the resistances in the following order \[{R_B} > {R_A} > {R_C}\]

Note: Metals are fine electricity conductors. They, therefore, have low resistivity. In comparison with metallic conductors, insulators such as rubber, glass, graphite, plastics, etc. have very high resistivity. The third form is the semiconductor that comes between the insulators and the conductors. With the rise in temperature, their resistivity decreases and is also affected by the presence of impurities in them.