Question

The equivalent resistance for the ‘n’ resistors with resistance R connected in parallel is
$
  {\text{(A) nR}} \\
  {\text{(B) R}} \\
  {\text{(C) }}\dfrac{{\text{R}}}{{\text{n}}} \\
  {\text{(D) n}}{{\text{R}}^{\text{2}}} \\
$

Answer 1

Hint:For evaluating equivalent resistance for n number of resistors in parallel combination, use ohm’s law and substitute the value of current through each resistor there. In parallel, the potential difference is the same (constant).

Complete step by step solution:The circuit diagram for the n number of resistors connected in parallel combination is as shown:

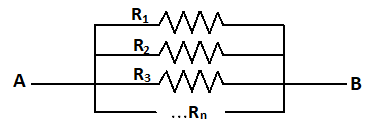
Let us consider that ${{\text{I}}_{\text{1}}}$current flows through resistor ${{\text{R}}_{\text{1}}}$
Let ${{\text{I}}_{\text{2}}}$current flows through resistor through resistor ${{\text{R}}_{\text{2}}}$
And let ${{\text{I}}_3}$current flows through resistor through resistor ${{\text{R}}_3}$
And R = resistance of the conductor
Total current in the circuit is given by
${\text{I = }}{{\text{I}}_{\text{1}}}{\text{ + }}{{\text{I}}_{\text{2}}}{\text{ + }}{{\text{I}}_{\text{3}}}...{\text{(i)}}$
According to the ohm’s law, the current flowing through a conductor is directly proportional to the potential difference across the ends of the conductor provided that the physical conditions like temperature, pressure of the conductor remain constant.
${\text{V = IR}}$
Or ${\text{I = }}\dfrac{{\text{V}}}{{\text{R}}}$
Where V = potential difference applied across the ends of the conductor
I = current flowing through the conductor
In parallel, potential difference (V) is the same.
For current ${{\text{I}}_{\text{1}}}$
${{\text{I}}_{\text{1}}}{\text{ = }}\dfrac{{\text{V}}}{{{{\text{R}}_{\text{1}}}}}$
For current ${{\text{I}}_{\text{2}}}$
${{\text{I}}_2}{\text{ = }}\dfrac{{\text{V}}}{{{{\text{R}}_2}}}$
For current ${{\text{I}}_{\text{3}}}$
${{\text{I}}_3}{\text{ = }}\dfrac{{\text{V}}}{{{{\text{R}}_3}}}$
Now substituting the values of c${{\text{I}}_{\text{1}}}{\text{, }}{{\text{I}}_{\text{2}}}{\text{ and }}{{\text{I}}_{\text{3}}}$current, we get
$
  \dfrac{{\text{V}}}{{{{\text{R}}_{\text{p}}}}}{\text{ = }}\dfrac{{\text{V}}}{{{{\text{R}}_{\text{1}}}}}{\text{ + }}\dfrac{{\text{V}}}{{{{\text{R}}_{\text{2}}}}}{\text{ + }}\dfrac{{\text{V}}}{{{{\text{R}}_{\text{3}}}}} \\
   \Rightarrow \dfrac{{\text{1}}}{{{{\text{R}}_{\text{p}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{1}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{2}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{3}}}}} \\
$
For n number of resistors
$\dfrac{{\text{1}}}{{{{\text{R}}_{\text{n}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{1}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{2}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{3}}}}}{\text{ + }}...{\text{ + }}\dfrac{{\text{1}}}{{{{\text{R}}_{\text{n}}}}}$
According to the question, resistance for the ‘n’ resistors have resistance R.
$\therefore {\text{ }}{{\text{R}}_{\text{1}}}{\text{ = }}{{\text{R}}_{\text{2}}}{\text{ = }}{{\text{R}}_{\text{3}}}{\text{ = }}.........{\text{ = }}{{\text{R}}_{\text{n}}}{\text{ = R}}$
So, ${{\text{R}}_{\text{p}}}{\text{ = }}\dfrac{{\text{R}}}{{\text{n}}}$
The equivalent resistance for the ‘n’ resistors with resistance R connected in parallel is$\dfrac{{\text{R}}}{{\text{n}}}$.

Therefore, option (C) is the correct choice.

Note:Similarly, we can find the equivalent resistance for the ‘n’ resistors with resistance R connected in series combination using ohm’s law. But keep in mind that in series combination the value of current is the same (constant).