Question

The equivalent capacity between A and B in the given circuit is (\[{{\text{C}}_{\text{1}}} = 4 \mu F \], \[{{\text{C}}_{\text{2}}} = 12 \mu F \], \[{{\text{C}}_{\text{3}}} = 8 \mu F \], \[{{\text{C}}_{\text{4}}} = 4 \mu F \], \[{{\text{C}}_{\text{5}}} = 8 \mu F \])

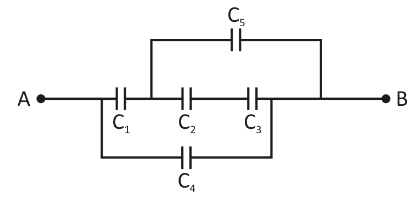
A. \[24\mu F\]
B. \[36\mu F\]
C. \[\dfrac{{16}}{3}\mu F\]
D. \[\dfrac{8}{3}\mu F\]

Answer 1

Hint: In this question, the given figure can be represented or drawn as the balance wheatstone bridge. Find the capacitance of the upper arm and the lower arm of the circuit then by using both capacitance find the equivalent capacitance of the circuit.

Complete step by step answer:
The given figure can be redrawn into equivalent circuit as shown:

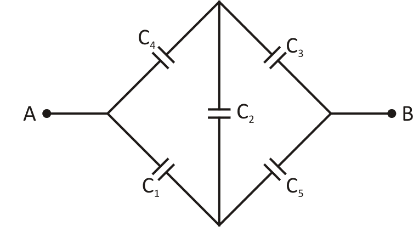
Here, the wheatstone bridge is balanced. So,\[12\mu F\] becomes ineffective. Capacitance of the upper arm and \[{C_3}\] are in series, \[\dfrac{1}{{{C_U}}} = \dfrac{1}{{{C_4}}} + \dfrac{1}{{{C_3}}}\]

Where ${C_U}$ is the upper arm capacitance and
\[{{\text{C}}_{\text{1}}} = 4 \mu F\] , \[{{\text{C}}_{\text{2}}} =12 \mu F\],
\[{{\text{C}}_{\text{3}}} = 8 \mu F\], \[{{\text{C}}_{\text{4}}} = 4 \mu F \], \[{{\text{C}}_{\text{5}}} = 8 \mu F \]
\[\dfrac{1}{{{C_U}}} = \dfrac{1}{4} + \dfrac{1}{8} \\
\Rightarrow\dfrac{1}{{{C_U}}} = \dfrac{{2 + 1}}{8}\\
\Rightarrow\dfrac{1}{{{C_U}}} = \dfrac{3}{8}\mu F\]
\[\Rightarrow {C_U} = \dfrac{8}{3}\mu F\]

Capacitance of the lower arm is \[{C_1}\] and \[C{}_5\] are in series,
\[\dfrac{1}{{{C_L}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_5}}}\]
\[\Rightarrow\dfrac{1}{{{C_L}}} = \dfrac{1}{4} + \dfrac{1}{8} \\
\Rightarrow\dfrac{1}{{{C_L}}} = \dfrac{{2 + 1}}{8}\\
\Rightarrow\dfrac{1}{{{C_L}}} = \dfrac{3}{8}\mu F\]
\[\Rightarrow{C_L} = \dfrac{8}{3}\mu F\]

${C_L}$ is the lower arm capacitance. Now, \[{C_U}\] and \[{C_L}\] are in parallel.
The equivalent capacitance ${C_{eq}}$ between points A and B is
\[{C_{eq}} = {C_U} + {C_L}\]
\[\Rightarrow{C_{eq}} = \dfrac{8}{3} + \dfrac{8}{3} \\
\therefore{C_{eq}}= \dfrac{{16}}{3}\mu F\]

Hence, option C is correct.

Note:In this question we are asked to find the equivalent capacitance of the given circuit. Here, we redraw the figure as a balance wheatstone bridge and solve the question step by step and first try to find capacitance of upper arm then lower arm. So, we are able to find out the total equivalent capacitance of the circuit. Without finding the upper arm and lower arm capacitance we cannot find the equivalent capacitance.