Question

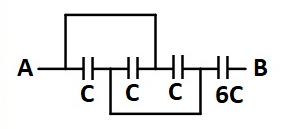
The equivalent capacitance between A and B is

(A)C
(B) 3C
(C) 9C
(D) 2C

Answer 1

Hint: For finding equivalent capacitance of the network, check the connections made i.e. capacitances which are in series combination and in parallel combination. Then apply the formula for net capacitance which is for series, the formula for net capacitance is given as
$\dfrac{{\text{1}}}{{{{\text{C}}_{{\text{net}}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{1}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{2}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{3}}}}}{\text{ + }}....{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{n}}}}}$
And for parallel combination, the formula for net capacitance is given as
${{\text{C}}_{{\text{net}}}}{\text{ = }}{{\text{C}}_{\text{1}}}{\text{ + }}{{\text{C}}_{\text{2}}}{\text{ + }}{{\text{C}}_{\text{3}}}{\text{ + }}....{\text{ + }}{{\text{C}}_{\text{n}}}$

Complete step by step solution:
First three capacitors having capacitance C each are arranged in parallel combination and last capacitor having capacitance 6 C is arranged in series with them.
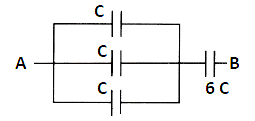
Equivalent diagram is shown below

Now, finding capacitance for first 3 capacitors having capacitance C each arranged in parallel combination. The formula for parallel combination, the formula for net capacitance is given as
${{\text{C}}_{{\text{net}}}}{\text{ = }}{{\text{C}}_{\text{1}}}{\text{ + }}{{\text{C}}_{\text{2}}}{\text{ + }}{{\text{C}}_{\text{3}}}{\text{ + }}....{\text{ + }}{{\text{C}}_{\text{n}}}$
Here, only three capacitances are there so formula can be written as
${{\text{C}}_{{\text{net}}}}{\text{ = }}{{\text{C}}_{\text{1}}}{\text{ + }}{{\text{C}}_{\text{2}}}{\text{ + }}{{\text{C}}_{\text{3}}}$
According to the question, ${{\text{C}}_{\text{1}}}{\text{ = }}{{\text{C}}_{\text{2}}}{\text{ = }}{{\text{C}}_{\text{3}}}{\text{ = C}}$
Now substituting the value of C₁, C₂ and C₃ in the above formula, we get
$
  {{\text{C}}_{{\text{net}}}}{\text{ = C + C + C}} \\
  \therefore {{\text{C}}_{{\text{net}}}}{\text{ = 3C}} \\
$
Now, capacitor having capacitance is arranged in series combination with${{\text{C}}_{{\text{net}}}}$.
For series combination, the formula for net capacitance is given as
$\dfrac{{\text{1}}}{{{\text{C}}{{\text{'}}_{{\text{net}}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{1}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{2}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{3}}}}}{\text{ + }}....{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{n}}}}}$
Here, only two capacitances are there so formula can be written as
$\dfrac{{\text{1}}}{{{{\text{C}}_{{\text{net}}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{1}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{{\text{C}}_{\text{2}}}}}$
According to the question, $\dfrac{{\text{1}}}{{{\text{C}}{{\text{'}}_{{\text{net}}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{{\text{C}}_{{\text{net}}}}}}{\text{ + }}\dfrac{{\text{1}}}{{{\text{6C}}}}$
Substituting the value of ${{\text{C}}_{{\text{net}}}}$in above formula, we get
 $
  \dfrac{{\text{1}}}{{{\text{C}}{{\text{'}}_{{\text{net}}}}}}{\text{ = }}\dfrac{{\text{1}}}{{{\text{3C}}}}{\text{ + }}\dfrac{{\text{1}}}{{{\text{6C}}}} \\
   \Rightarrow \dfrac{{\text{1}}}{{{\text{C}}{{\text{'}}_{{\text{net}}}}}}{\text{ = }}\dfrac{{\text{3}}}{{{\text{6C}}}} \\
   \Rightarrow \dfrac{{\text{1}}}{{{\text{C}}{{\text{'}}_{{\text{net}}}}}}{\text{ = }}\dfrac{1}{{{\text{2C}}}} \\
  \therefore {\text{ C}}{{\text{'}}_{{\text{net}}}} = {\text{2C}} \\
$
So, the equivalent capacitance between A and B is 2C.

Therefore, option (D) is the correct choice.

Note:
Capacitance is the ability of a capacitor to store the charge.When charge is given to a conductor then its potential increases. SI unit of capacitance is farad (abbreviated F). CGS unit of capacitance is statfarad (abbreviated statF).