Question

The equations of diagonals of the square formed by the lines x=0, y=0, x=1, y=1 are-

Answer 1

Hint: To solve this problem, first find the coordinates of the vertices of the square and then find the diagonals using those points using the equation-
\[\mathrm y-{\mathrm y}_1=\dfrac{{\mathrm y}_2-{\mathrm y}_1}{{\mathrm x}_2-{\mathrm x}_1}\left(\mathrm x-{\mathrm x}_1\right)\]

Complete step-by-step answer:

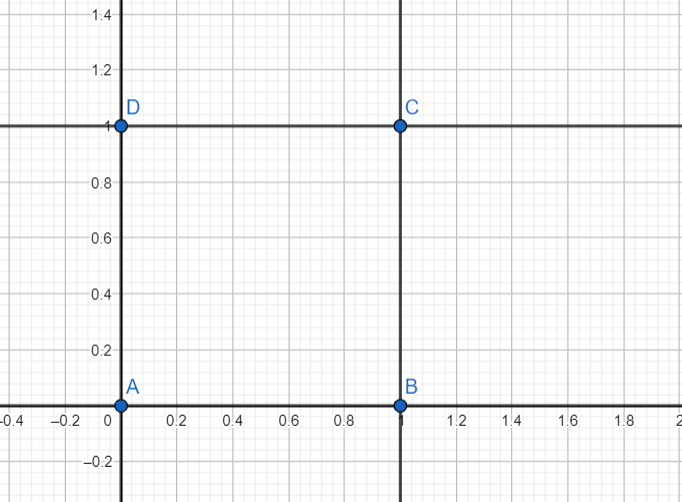
From the equations, it is clear that the vertices of the square are-
A(0,0), B(1,0), C(1,1), D(0,1)
To find the diagonals, we have to find the equations of the line AC and BD.
For line AC, we can write that-
\[\mathrm y-0=\dfrac{1-0}{1-0}\left(\mathrm x-0\right)\\\mathrm y=\mathrm x\\\mathrm x-\mathrm y=0\]
For line BD, we can write that-
\[\mathrm y-0=\dfrac{1-0}{0-1}\left(\mathrm x-1\right)\\\mathrm y=-\mathrm x+1\\\mathrm x+\mathrm y-1=0\]

These are the required equations of the diagonals.

Note: We can also use the form y=mx+c to find the equation of the lines, where m is the slope and c is the y-intercept. For AC, slope is clearly 1 and intercept is 0, so equation becomes-
y=x
For BD, slope is -1 and intercept is 1, so equation becomes-
y=-x+1
x+y-1=0