Question

The equation $x\log x = 3 - x$ has at least one root in the interval ______?

Answer 1

Hint:
The solution of the equation: $x\log x = 3 - x$ will be given by the point of intersection of the two graphs $y = x\log x$ and $y = 3 - x$.
The graph of function $y = 3 - x$ will be a straight line with intercepts $\left( {3,0} \right){\text{ and }}\left( {0,3} \right)$.
For drawing graph of function $y = x\log x$:
First find its x-intercept by equating $f\left( x \right) = 0$.
And then find where it is increasing and decreasing function by checking the sign of $f'\left( x \right)$about critical points.
Check where the two curves intersect and find the range of intervals.

Complete step by step solution:
This question can be solved graphically.
First, we will have to draw the graphs of functions $y = x\log x$ and $y = 3 - x$.
The solution of the equation: $x\log x = 3 - x$ will be given by the point of intersection of the two graphs.
 It will help us to find in which interval the graphs intersect, or the solution exists.
1. Drawing graph of function $y = x\log x$ :
The domain of this function $f\left( x \right) = x\log x$ is $\left( {0,\infty } \right)$since $\log x$ is only defined for $x > 0$.
Now, finding the x-intercepts of the graph, putting $f\left( x \right) = 0,$ we get:
$ \Rightarrow x\log x = 0$
$
   \Rightarrow x = 0{\text{ or }}\log x = 0 \\
   \Rightarrow x = 0{\text{ or }}x = 1 \\
 $
Checking the monotonicity of the function:
$
  \because f\left( x \right) = x\log x \\
   \Rightarrow f'\left( x \right) = 1 + \log x \\
 $
Putting $f'\left( x \right) = 0$, for finding the critical points:
$
   \Rightarrow 1 + \log x = 0 \\
   \Rightarrow \log x = - 1 \\
   \Rightarrow x = {e^{ - 1}} = \dfrac{1}{e} \\
 $
We can easily check that for $x > \dfrac{1}{e}$, the value of $f'\left( x \right)$ is positive, hence function is increasing here.
And similarly, for $x < \dfrac{1}{e}$, the value of $f'\left( x \right)$ is negative, hence function is decreasing here.

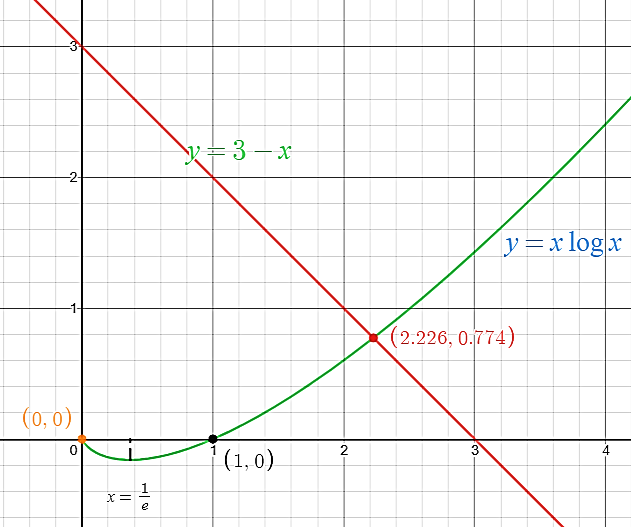
2. Drawing graph of function $y = 3 - x$:
It is a straight line with x-intercept: $\left( {3,0} \right)$
And y-intercept: $\left( {0,3} \right)$
From the graph shown above, we can clearly see that the two functions intersect at a point between $x = 1$and $x = 3$.

Hence the equation $x\log x = 3 - x$ has at least one root in the interval $\left( {1,3} \right)$.

Note:
The value of $\log x$ for $x = 0$ is undefined. Because from the basic definition of logarithm:
$y = {\log _b}a$, the value of y is equal to that exponent of base ‘b’ which on applying on the base ‘b’ gives value ‘a’.
I.e. if ${b^k} = a$, then $y = k$.
Now, if we think for a = 0, there is no exponent k which can make ${b^k} = 0$.
Hence, logarithm is only defined for a>0.