Question

The equation of the director circle of the hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] is:
(a) \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\]
(b) \[{{x}^{2}}+{{y}^{2}}={{b}^{2}}\]
(c) \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}+{{b}^{2}}\]
(d) \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{b}^{2}}\]

Answer 1

Hint: First of all, draw a hyperbola and two perpendicular tangents to it and name the point of their intersection as P (h, k) which is the locus of its director circle. Now, write the equation of the tangent of the hyperbola as \[y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}-{{b}^{2}}}\] and substitute x = h and y = k. Now, substitute the product of roots that is \[{{m}_{1}}{{m}_{2}}=-1\] after squaring both the sides and making a quadratic equation in terms of m.

Complete step-by-step answer:

In this question, we have to find the director of the circle of the hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]. We know that the director of any circle is the locus of its point of intersection of the perpendicular tangents. So, first of all, let us draw the hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] and name the point of intersection of its perpendicular tangents as P (h, k).

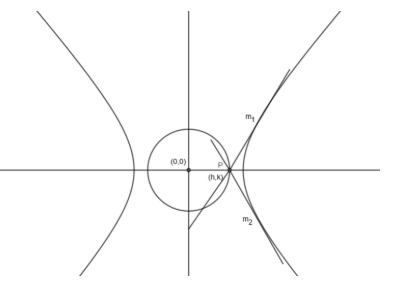
Let the slopes of the two tangents be \[{{m}_{1}}\] and \[{{m}_{2}}\]. In hyperbola, we know that the equation of the tangent is given by \[y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}-{{b}^{2}}}\] where m is the slope of the tangent. We can also write the above tangent as
\[y-mx=\pm \sqrt{{{a}^{2}}{{m}^{2}}-{{b}^{2}}}\]
We know that the above tangent is passing from P (h, k). So by substituting x = h and y = k, we get,
\[k-mh=\pm \sqrt{{{a}^{2}}{{m}^{2}}-{{b}^{2}}}\]
By squaring both the sides of the above equation, we get,
\[{{\left( k-mh \right)}^{2}}={{a}^{2}}{{m}^{2}}-{{b}^{2}}\]
By using the formula \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\], we get,
\[{{k}^{2}}+{{m}^{2}}{{h}^{2}}-2mkh={{a}^{2}}{{m}^{2}}-{{b}^{2}}\]
By rearranging the terms of the above equation, we get,
\[{{m}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)-2mkh+{{k}^{2}}+{{b}^{2}}=0\]
Above is the quadratic equation in m and we know that the roots of this quadratic equation are \[{{m}_{1}}\] and \[{{m}_{2}}\]. We know that the product of the roots \[=\dfrac{c}{a}=\dfrac{\text{coefficient of }{{\text{m}}^{0}}}{\text{coefficient of }{{\text{m}}^{2}}}\]
So, we get,
\[{{m}_{1}}{{m}_{2}}=\dfrac{{{k}^{2}}+{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}}....\left( i \right)\]
We know that when two lines are perpendicular, the product of their slopes is – 1. As we know that the given tangents are also perpendicular, so we get, \[{{m}_{1}}{{m}_{2}}=-1....\left( ii \right)\]
By equating equation (i) and (ii), we get,
\[\dfrac{{{k}^{2}}+{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}}=-1\]
By cross multiplying the above equation, we get,
\[{{k}^{2}}+{{b}^{2}}=-{{h}^{2}}+{{a}^{2}}\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}={{a}^{2}}-{{b}^{2}}\]
By replacing h by x and k by y, we get,
\[{{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{b}^{2}}\]
So, we get the equation of the director circle of the hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] as \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{b}^{2}}\].
Hence, option (d) is the right answer.

Note: In this question, students must note that this definition of the director circle is true for every curve and not only for the hyperbola. Also, students must remember the equation of the director circle of the same general curves as hyperbola, ellipse, circle, etc. Some students often make a mistake while writing the product of the roots as \[\dfrac{-b}{a}\] in the above question. So this mistake must be taken care of.