Question

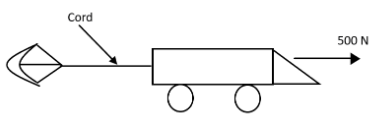
The engine of an 800 kg sports car exerts a constant force of 500 N on the car. When the parachute is opened, the car decelerates at $ 2.5m{s^{ - 2}} $ , while the engine continues to provide the forward force of 500 N. What is the tension in the cord at the instant? (assuming that there is no other resistive force.)

(A) 500 N
(B) 1500N
(C) 2000 N
(D) 2500 N

Answer 1

Hint: Newton’s second law of motion states that the net force exerted on a body is directly proportional to the mass of the body and acceleration of its motion. The tension force exerts a back force on the car. So by setting the equation of motion of the car, we can find the tension on the cord.

Formula used: In this solution we will be using the following formulae;
$ {F_{NET}} = ma $ , where $ {F_{NET}} $ is the sum of the vector sum forces acting on the body, $ m $ is the mass of the body and $ a $ is the acceleration.

Complete step by step solution:
When the parachute opens, the string becomes taut and thus exerts a tension force on the car. This tension force opposes the forward force exerted by the engine on the car, so that it slows down the engine.
This tension force causes a deceleration of $ 2.5m{s^{ - 2}} $ as mentioned above. Hence, the Tension force is greater than the engine force.
Applying Newton’s second law, we have that
 $\Rightarrow {F_{NET}} = T - {F_g} = ma $ (taking the leftward direction positive) where $ {F_g} $ is the force of the engine exerted to move the car forward.
Inserting known values from the question, we have
 $\Rightarrow {F_{NET}} = T - 500 = 800(2.5) $
Thus to find the tension,
 $\Rightarrow T = 800(2.5) + 500 = 2500N $
Therefore the tensional force on the string is 2500 N.
Hence the correct answer is option D.

Note:
Alternatively, we can also assume forward (rightward direction) direction is positive as in
 $\Rightarrow {F_{NET}} = {F_g} - T = - ma $ The acceleration is negative because the car is decelerating meaning that the acceleration of the car is backwards. We say this because, if the force is continuously exerted on the car, the car will decelerate to zero after which it actually starts to accelerate backwards.
Proceeding and making $ T $ subject of the formula from $ {F_{NET}} = {F_g} - T = - ma $ , we have
 $\Rightarrow T = ma + {F_g} = 800(2.5) + 500 = 2500N $
This is identical to the answer gotten in solution.