Question

The energy required to excite an electron from $n=2$ to $n=3$ energy state is $47.2eV$. The atomic number of the nucleus, around which the electron is revolving will be
$\begin{align}
  & A)5 \\
 & B)10 \\
 & C)15 \\
 & D)20 \\
\end{align}$

Answer 1

Hint: Energy required for excitation of electrons from one orbit to another orbit in a nucleus is equal to the difference in energies of electrons at those particular orbits. Energy of an electron in a particular orbit is dependent on the atomic number of the nucleus, around which the electron is revolving.

Formula used:
$1){{E}_{n}}=\dfrac{13.6{{Z}^{2}}}{{{n}^{2}}}$
\[2)\Delta E=13.6{{Z}^{2}}\left( \dfrac{1}{{{n}_{1}}^{2}}-\dfrac{1}{{{n}_{2}}^{2}} \right)\]

Complete step by step answer:
We know that electrons move randomly inside a nucleus. We also know that electrons revolve in orbits around the nucleus. Energy of an electron inside a nucleus is given by
${{E}_{n}}=\dfrac{13.6{{Z}^{2}}}{{{n}^{2}}}$
where
${{E}_{n}}$ is the energy of an electron revolving around a nucleus
$Z$ is the atomic number of the nucleus around which the electron is revolving
$n$ is the orbit in which the electron is revolving around the nucleus
Let this be equation 1.
Sometimes, it occurs that electrons inside the nucleus jump from one orbit to another due to their random motion. Energy required by an electron to jump from one orbit to another orbit inside a nucleus is given by
\[\Delta E={{E}_{{{n}_{1}}}}-{{E}_{{{n}_{2}}}}=\dfrac{13.6{{Z}^{2}}}{{{n}_{1}}^{2}}-\dfrac{13.6{{Z}^{2}}}{{{n}_{2}}^{2}}=13.6{{Z}^{2}}\left( \dfrac{1}{{{n}_{1}}^{2}}-\dfrac{1}{{{n}_{2}}^{2}} \right)\]
where
$\Delta E$ is the energy required by an electron to jump from ${{n}_{1}}$ to ${{n}_{2}}$
${{n}_{1}}$ is the orbit from which the electron jumps
${{n}_{2}}$ is the orbit to which the electron jumps
Let this be equation 2.
The following energy level diagram of Hydrogen (Z=1) can be used to clarify the formula of excitation energy in equation 2.

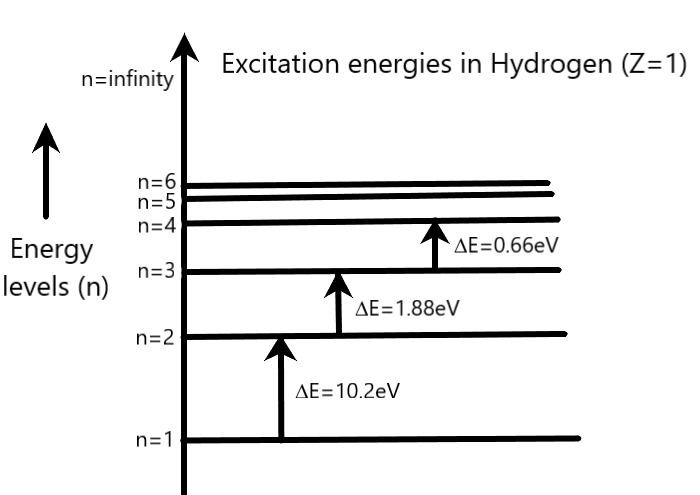
Coming to our question, we are given that the electron is jumping from second orbit to third orbit. Therefore, we can write
$\begin{align}
  & {{n}_{1}}=2 \\
 & {{n}_{2}}=3 \\
\end{align}$
Also, the energy required by the electron to jump from ${{n}_{1}}$ to ${{n}_{2}}$ is given as $47.2eV$. Therefore, we can write
$\Delta E=47.2eV$
We are required to find the atomic number of the nucleus, $Z$, around which the given electron is moving. To find the same, equation 2 can be rearranged as
\[\Delta E=13.6{{Z}^{2}}\left( \dfrac{1}{{{n}_{1}}^{2}}-\dfrac{1}{{{n}_{2}}^{2}} \right)\Rightarrow Z={{\left( \dfrac{\Delta E}{13.6\left( \dfrac{1}{{{n}_{1}}^{2}}-\dfrac{1}{{{n}_{2}}^{2}} \right)} \right)}^{\dfrac{1}{2}}}\]
Substituting the given values in the above expression, we have
\[Z={{\left( \dfrac{\Delta E}{13.6\left( \dfrac{1}{{{n}_{1}}^{2}}-\dfrac{1}{{{n}_{2}}^{2}} \right)} \right)}^{\dfrac{1}{2}}}={{\left( \dfrac{47.2eV}{13.6eV\left( \dfrac{1}{{{2}^{2}}}-\dfrac{1}{{{3}^{2}}} \right)} \right)}^{\dfrac{1}{2}}}={{\left( \dfrac{47.2eV}{13.6eV\left( \dfrac{1}{4}-\dfrac{1}{9} \right)} \right)}^{\dfrac{1}{2}}}\]
On further simplification, we have
\[Z={{\left( \dfrac{47.2eV}{13.6eV\left( \dfrac{1}{4}-\dfrac{1}{9} \right)} \right)}^{\dfrac{1}{2}}}={{\left( \dfrac{47.2eV}{13.6eV\left( \dfrac{5}{36} \right)} \right)}^{\dfrac{1}{2}}}={{\left( \dfrac{47.2eV}{1.88eV} \right)}^{\dfrac{1}{2}}}=\sqrt{25}=5\]
Therefore, the atomic number of the nucleus around which the given electron is revolving is equal to $5$. Hence, the correct answer is option $A$.

Note:
If students can remember the formula given in equation 2, they can easily approach the problem without wasting much time. But it should be kept in mind that they can always derive the excitation energy required by an electron from equation 1, as done in the above solution. Students should also take care while substituting the values for ${{n}_{1}}$ and ${{n}_{2}}$.
${{n}_{1}}$ is the orbit from which the electron jumps.
${{n}_{2}}$ is the orbit to which the electron jumps.