Question

The energy of the electron of hydrogen atom in its nth orbit is given by ${{E}_{n}}=-\dfrac{13.6}{{{n}^{2}}}$ electron volt (eV). Based on this formula.
a.) Draw different energy levels corresponding to \[n\text{ }=\text{ }1,2,3,4,5,6...\infty \].
b.) Show Lyman and Baler series of emission spectrum of hydrogen atom by drawing various electronic transitions.
c.) Find the ionization energy of a hydrogen atom.

Answer 1

Hint: For the hydrogen spectrum series, use the Rydberg formula as the expression for the energy level of each state. For different energy levels corresponding to varying n, calculate the values and draw Lyman and Balmer series, which is the electron from a higher energy state jumps onto $n=1$ and $n=2$ for Lyman and Balmer series respectively.

Complete step-by-step answer:
(i) In 1914, Niels Bohr proposed a theory of hydrogen. The excitement in an atom (in this case Hydrogen, with one electron only) is determined by the position of its electron. The higher the number of orbits the electron resides in; more is its energy. The expression for the energy is given by:

${{E}_{n}}=-\dfrac{13.6}{{{n}^{2}}}$

So, the energy of electron in different states or levels can be calculated as:

\[\begin{align}
  & {{E}_{1}}=-\dfrac{13.6}{{{1}^{2}}}=-13.6eV \\
 & {{E}_{2}}=-\dfrac{13.6}{{{2}^{2}}}=-3.4eV \\
 & {{E}_{3}}=-\dfrac{13.6}{{{3}^{2}}}=-1.51eV \\
 & {{E}_{4}}=-\dfrac{13.6}{{{4}^{2}}}=-0.85eV \\
 & . \\
 & . \\
 & {{E}_{\infty }}=-\dfrac{13.6}{{{\infty }^{2}}}=0eV \\
\end{align}\]

(ii) The Lyman’s series corresponds to the transitions between the states with principal quantum number \[{{n}_{\text{final}}}=1\]and \[{{n}_{\text{initial}}}=2,3,4...\infty \]. Similarly, Lyman’s series corresponds to the transitions between the states with principal quantum number \[{{n}_{\text{final}}}=2\] and \[{{n}_{\text{initial}}}=3,4,5...\infty \]. The transitions for the series look like:

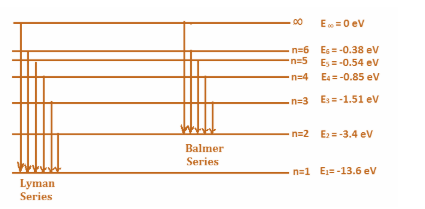
(iii) An atom is said to be ionized when an electron for the atom no longer stays in one of the energy levels of the atom. Or in other words, it reaches the state infinity. For a hydrogen atom, since there is only one electron, it resides in state $n=1$ and the final state is $n=\infty $. Therefore, the energy difference between the two states will give the ionization energy. That is:

$\begin{align}
  & {{E}_{\text{ionization}}}={{E}_{\infty }}-{{E}_{1}} \\
 & \Rightarrow 0-(-13.6)eV \\
 & {{E}_{\text{ionization}}}=13.6eV \\
\end{align}$

Note: It is important to understand that the energy level is always negative at any level, therefore, the magnitude of energy at a particular level might be more but the energy is less when the state is lower. Also note that the more energy an electron has, the more it is unstable, that is every electron wishes to jump to an energy level with lowest possible energy. This is also evident from the fact that for ionization, that is increasing the energy level to infinity, we had to provide energy in order to achieve it.