Question

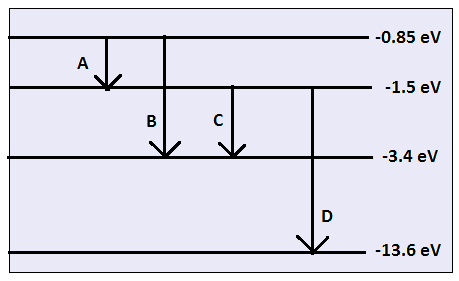
The energy level diagram of the given element is given below. Identify by doing necessary calculation which transition corresponds to the emission of a spectral line of wavelength 102.7 nm.

Answer 1

Hint: The amount of energy associated with the photon of radiation is directly proportional to the frequency of incident light which is expressed as $E = h\nu $. It shows that higher the frequency of incident light the higher the energy corresponds to photons.

Complete answer:
As we know the relation between energy of photon and frequency of incident light is $E = h\nu $.
Where is defined as a universal constant, known as planck's constant. Value of planck's constant is $6.626 \times {10^{ - 34}}$ Js.
 As we know frequency is also expressed in terms of light constant and wavelength of radiation.
$\nu = \dfrac{c}{\lambda }$
So, final equation of energy in terms of wavelength becomes-
$E = \dfrac{{hc}}{\lambda }$
For element A
${E_1} = - 1.5$
${E_2} = - 0.85$
Therefore, difference in energy is
$\Delta {\rm E} = \left( {{E_2} - {E_1}} \right)$
$\Delta {\rm E} = - 0.85 - \left( { - 1.5} \right)$
After solving the above equation, we get $\Delta {\rm E} = 0.65$
Now calculate the wavelength of transition
$\lambda = \dfrac{{hc}}{E}$
$\lambda = \dfrac{{6.626 \times {{10}^{ - 34}} \times 3.0 \times {{10}^8}}}{{0.65 \times 1.6 \times {{10}^{ - 19}}}}$
After solving this above equation, we get
$\lambda = 19.038 \times {10^{ - 7}}m$
In terms of nanometer value of wavelength is-
$\lambda = 1903.8nm$
For element B
${E_1} = - 3.4$
${E_2} = - 0.85$
Therefore, difference in energy is
$\Delta {\rm E} = \left( {{E_2} - {E_1}} \right)$
$\Delta {\rm E} = - 0.85 - \left( { - 3.4} \right)$
After solving the above equation, we get $\Delta {\rm E} = 2.55$
Now calculate the wavelength of transition
$\lambda = \dfrac{{hc}}{E}$
$\lambda = \dfrac{{6.626 \times {{10}^{ - 34}} \times 3.0 \times {{10}^8}}}{{2.55 \times 1.6 \times {{10}^{ - 19}}}}$
After solving this above equation, we get
$\lambda = 4.8529 \times {10^{ - 7}}m$
In terms of nanometer value of wavelength is-
$\lambda = 485.2nm$
For element C
${E_1} = - 3.4$
${E_2} = - 1.5$
Therefore, difference in energy is
$\Delta {\rm E} = \left( {{E_2} - {E_1}} \right)$
$\Delta {\rm E} = - 1.5 - \left( { - 3.4} \right)$
After solving the above equation, we get $\Delta {\rm E} = 1.9$
Now calculate the wavelength of transition
$\lambda = \dfrac{{hc}}{E}$
$\lambda = \dfrac{{6.626 \times {{10}^{ - 34}} \times 3.0 \times {{10}^8}}}{{1.9 \times 1.6 \times {{10}^{ - 19}}}}$
After solving this above equation, we get
$\lambda = 6.5131 \times {10^{ - 7}}m$
In terms of nanometer value of wavelength is-
$\lambda = 651nm$
For element D
${E_1} = - 13.6$
${E_2} = - 1.5$
Therefore, difference in energy is
$\Delta {\rm E} = \left( {{E_2} - {E_1}} \right)$
$\Delta {\rm E} = - 1.5 - \left( { - 13.6} \right)$
After solving the above equation, we get $\Delta {\rm E} = 12.1$
Now calculate the wavelength of transition
$\lambda = \dfrac{{hc}}{E}$
$\lambda = \dfrac{{6.626 \times {{10}^{ - 34}} \times 3.0 \times {{10}^8}}}{{12.1 \times 1.6 \times {{10}^{ - 19}}}}$
After solving this above equation, we get
$\lambda = 1.0227 \times {10^{ - 7}}m$
In terms of nanometer value of wavelength is-
$\lambda = 102.27nm$
Hence, from the above calculation transition of element D from $ - 1.5$ ev to $ - 13.6$ ev corresponds with the emission of wavelength of $102.27nm$.

Note:
Make sure to convert the wavelength of the radiation into nanometers and convert the unit of $\Delta {\rm E}$ from volts to electron-volts by multiplying it by $1.6 \times {10^{ - 19}}$.