Question

The ellipse \[{{\text{E}}_1}:\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 1\] is inscribed in a rectangle R whose sides are parallel to the coordinate axis. Another ellipse ${{\text{E}}_2}$ is passing through the point (0, 4) circumscribing the rectangle R. The eccentricity of the rectangle ${{\text{E}}_2}$ is
A. $\dfrac{{\sqrt 2 }}{2}$
B. $\dfrac{{\sqrt 3 }}{2}$
C. $\dfrac{1}{2}$
D. $\dfrac{3}{4}$

Answer 1

Hint: Here, first find the vertices of the ellipse \[{{\text{E}}_1}\] by comparing it with the standard equation. So you will get vertices of the rectangle. Assume the equation of ellipse ${{\text{E}}_2}$ and this ellipse must satisfy the point of the rectangle. Using points of the rectangle in second, find the values of its vertices and then apply formula to find eccentricity.

Complete step-by-step answer:
Given equation of ellipse \[{{\text{E}}_1}:\dfrac{{{x^2}}}{9} + \dfrac{{{y^2}}}{4} = 1\]

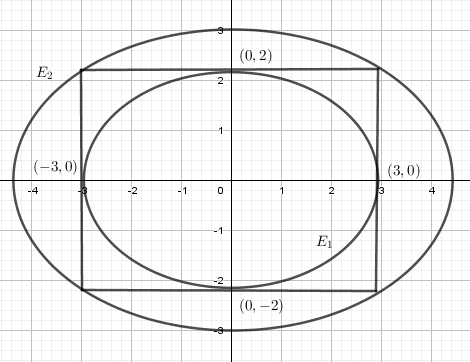
By comparing this equation as standard equation of ellipse i.e., \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] in which ellipse touches (± a,0) and y axis at (0,± b).
Therefore, the ellipse ${{\text{E}}_1}$ ​touches x-axis at (± 3,0) and y axis at (0,± 2).
 Also given that the ellipse is inscribed in rectangle R whose sides are parallel to the coordinate axis, then the vertices of the rectangle are (±3,±2).
Let the equation of ellipse \[{{\text{E}}_2}:\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]
The ellipse circumscribes the rectangle R, so the vertices of rectangle lie on ellipse ${{\text{E}}_2}$​
Therefore we get \[\dfrac{9}{{{a^2}}} + \dfrac{4}{{{b^2}}} = 1\]
Given that, the ellipse ${{\text{E}}_2}$​ passes through the point (0, 4).
So we get b = 4 and ${a^2} = 12$
For ellipse, we know that${a^2} = {b^2}(1 - {e^2})$, where e is the eccentricity of the ellipse.
⇒ $
  12 = 16(1 - {e^2}) \\
   \Rightarrow 1 - {e^2} = \dfrac{3}{4} \Rightarrow {e^2} = \dfrac{1}{4} \Rightarrow e = \dfrac{1}{2} \\
 $ ​
Therefore, the eccentricity of the rectangle ${{\text{E}}_2}$ is $\dfrac{1}{2}$.

Note: In these types of questions, first draw the clear diagram to see the given statement geometrically. Also all intersection points should be clearly visible. Always compare the given equation of ellipse with the standard equation and also assume any equation of ellipse as in the form of the standard equation. Also if any point is on the ellipse then it must satisfy the equation of ellipse use this fact to solve the problem.