Question

The electric potential existing in space is $V(x,y,z) = A\left( {xy + yz + xz} \right)$. If A is 10 SI units, find the magnitude of the electric field at (1,1,1).
A.)$20\sqrt 2 N/C$
B.)$20\sqrt 3 N/C$
C.)$10\sqrt 3 N/C$
D.)$20N/C$

Answer 1

Hint: Electric field is the gradient of electric potential. To find the potential, we need to take the derivative of potential along the direction of the electric field. This is easily obtained using the $\nabla $ operator: $\nabla = \dfrac{\partial }{{\partial x}}\hat i + \dfrac{\partial }{{\partial y}}\hat j + \dfrac{\partial }{{\partial z}}\hat k$. The electric Field $\vec E = \nabla (V)$

Complete step by step answer:
 We know the electric field at a point is defined as the gradient of the potential at that point.
$\vec E = - \dfrac{{dV}}{{dr}}\hat r$

But the $d\vec r$ should be along the direction of the electric field, which we do not know. But we know the electric field is always perpendicular to an equipotential surface. So the direction $d\vec r$ should be also along the perpendicular to equipotential.

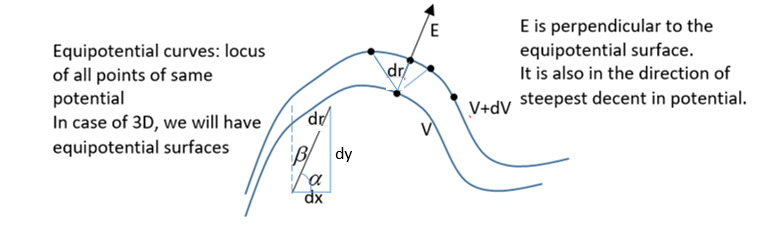
Since this perpendicular direction is also the direction in which potential varies the steepest, we can say $d\vec r$ should be taken along the direction of steepest change of potential.
Let's first find $\dfrac{{dV}}{{dr}}$ for some random direction, along a vector $\vec l = a\hat i + b\hat j + c\hat k$

So let's take the derivative of $V(x,y,z)$ for $dr$ along $d\vec l$
$\dfrac{{dV}}{{dr}} = \dfrac{{\partial V}}{{\partial x}}\dfrac{{dx}}{{dr}} + \dfrac{{\partial V}}{{\partial y}}\dfrac{{dy}}{{dr}} + \dfrac{{\partial V}}{{\partial z}}\dfrac{{dz}}{{dr}} = A\left( {(y + z)\dfrac{{dx}}{{dr}} + (x + z)\dfrac{{dy}}{{dr}} + (y + x)\dfrac{{dz}}{{dr}}} \right)$

Now, if we are moving a very small distance along $l$, the ratio : $\dfrac{{dx}}{{dr}} = \dfrac{{\text{adjacent}}}{\text{hypotenuse}} = cos\alpha$ where $\alpha $ is the angle of $l$ or $dr$ with X axis.

Similarly, we can find the rest as:
$\dfrac{{dy}}{{dr}} = cos\beta $
$\dfrac{{dz}}{{dr}} = cos\gamma $
Let's now substitute these values into equation (1).
$\dfrac{{dV}}{{dr}} = A\left( {(y + z)cos\alpha + (x + z)cos\beta + (y + x)cos\gamma } \right)$
This result can be rewritten as a dot product.

$\dfrac{dV}{dr}=A\left( (y+z)\hat{i}+(x+z)\hat{j}+(y+x)\hat{k} \right)\ \centerdot \ \left( cos\alpha \hat{i}+cos\beta \hat{j}+cos\gamma \hat{k} \right)$
We can replace $\left( cos\alpha \hat{i}+cos\beta \hat{j}+cos\gamma \hat{k} \right)$ as $\hat{l}$ Since both are a unit vector
$\dfrac{dV}{dr}=A\left( (y+z)\hat{i}+(x+z)\hat{j}+(y+x)\hat{k} \right)\ \centerdot \ \hat{l}$

Now, the electric field is in that direction in which this dot product is maximum ($\vec E$ varies the steepest). But we know the dot product of two vectors would be maximum if both vectors are along the same direction.
That means the steepest descent occurs when $l$ is along\[\left( {(y + z)\hat i + (x + z)\hat j + (y + x)\hat k} \right)\]
So the electric field is in this direction.

So the electric field can be given as :
$\vec E = - \dfrac{{dV}}{{dr}} = - A\left( {(y + z)\hat i + (x + z)\hat j + (y + x)\hat k} \right)$

We can Substitute the values (1,1,1) for x, y and z to find the electric field.
\[\vec E = - 10\left( {(1 + 1)\hat i + (1 + 1)\hat j + (1 + 1)\hat k} \right) = - 2\hat i - 2\hat j - 2\hat k\]
So the magnitude of is \[10\sqrt {{2^2} + {2^2} + {2^2}} = 20\sqrt 3 N/C\]. So the correct answer is option B.

Note: We can remember the operator $\vec \nabla = \dfrac{\partial }{{\partial x}}\hat i + \dfrac{\partial }{{\partial y}}\hat j + \dfrac{\partial }{{\partial z}}\hat k$ called the gradient operator. The electric field can be found easily by taking the negative gradient of V using the above formula.

$\vec E = - \vec \nabla V = - \left( {\dfrac{{\partial V}}{{\partial x}}\hat i + \dfrac{{\partial V}}{{\partial y}}\hat j + \dfrac{{\partial V}}{{\partial z}}\hat k} \right)$

Solution to this problem is complicated and not expected to be solved by higher secondary students. Such questions are added to consume the limited time given to us. Attempt such questions only If you are aiming for top ranks or If you know the final formula by-heart.