Question

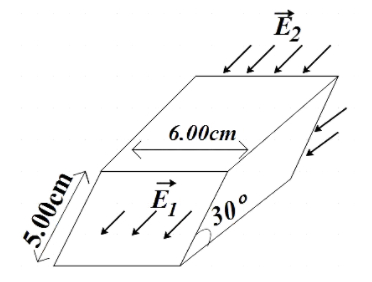
The electric field $\overrightarrow{{{E}_{1}}}$ at one face of a parallelepiped is uniform over the entire face and is directed out of the face. At the opposite face, the electric field $\overrightarrow{{{E}_{2}}}$ is also uniform over the entire face and is directed into that face (as shown in figure). The two faces in question are inclined at $30{}^\circ $ from the horizontal, $\overrightarrow{{{E}_{1}}}$ and$\overrightarrow{{{E}_{2}}}$ (both horizontal) have magnitudes of $2.50\times {{10}^{4}}N/C$ and$7.00\times {{10}^{4}}N/C$, respectively. Assuming that no other electric field lines cross the surfaces of the parallelepiped, the net charge contained within is

Answer 1

Hint: You could first find the electric flux passing through each face by recalling the expression for it in terms of the given quantities. Then, you could find the net flux by adding the flux through the two surfaces. Now you could make use of the Gauss’s law to get the net charge enclosed within the closed surface and hence the answer.
Formula used:
Electric flux,
${{\phi }_{E}}=\overrightarrow{E}\centerdot \overrightarrow{A}=EA\cos \theta $
Gauss’s law,
${{\phi }_{E}}=\dfrac{1}{{{\varepsilon }_{0}}}{{Q}_{en}}$

Complete answer:
We know that, when the electric field is uniform, the electric flux passing through a surface of vector area A is given by,
${{\phi }_{E}}=\overrightarrow{E}\centerdot \overrightarrow{A}=EA\cos \theta $ ………………………….. (1)
Where,
E = the magnitude of electric field
A = the area of the surface
$\theta $ = the angle between the electric field lines and the normal to the surface A
${{\phi }_{E}}$ = flux of the electric field through a closed surface
Now let us consider the surface through which $\overrightarrow{{{E}_{1}}}$ is coming out. We are told that the electric field is inclined at $30{}^\circ $with horizontal. So, quite obviously, angle made by the electric field with the normal will be,
$\theta =90-30=60{}^\circ $ ………………………………. (2)
Area of the surface,
$A=5\times {{10}^{-2}}\times 6\times {{10}^{-2}}=30{{m}^{2}}$ ……………………………… (3)
Magnitude of electric field is given as,
$\left| \overrightarrow{{{E}_{1}}} \right|={{E}_{1}}=2.50\times {{10}^{4}}N/C$ ………………………………… (4)
Substituting (2), (3) and (4) in (1), we get,
${{\phi }_{{{E}_{1}}}}={{E}_{1}}A\cos 60{}^\circ $
$\Rightarrow {{\phi }_{{{E}_{1}}}}=2.50\times {{10}^{4}}\times 30\times \dfrac{1}{2}$
$\therefore {{\phi }_{{{E}_{1}}}}=37.5\times {{10}^{4}}N{{m}^{2}}/C$
Now, let us find the flux for the other surface where $\overrightarrow{{{E}_{2}}}$ is going in. The inclination here is also $30{}^\circ $ with the horizontal, so the angle made by the electric field with the normal of the surface will be,
$\theta =90+30=120{}^\circ $
Magnitude of electric field is given as,
$\left| \overrightarrow{{{E}_{2}}} \right|=7.00\times {{10}^{4}}N/C$
The surface area is same as the above case, so, the flux could be given by,
${{\phi }_{{{E}_{2}}}}={{E}_{2}}A\cos 120{}^\circ $
$\Rightarrow {{\phi }_{{{E}_{2}}}}=7.00\times {{10}^{4}}\times 30\times \left( -\dfrac{1}{2} \right)$
$\therefore {{\phi }_{{{E}_{2}}}}=-105\times {{10}^{4}}N{{m}^{2}}/C$
Total flux through the given closed surface is given by,
${{\phi }_{E}}={{\phi }_{{{E}_{1}}}}+{{\phi }_{{{E}_{2}}}}$
$\Rightarrow {{\phi }_{E}}=37.5\times {{10}^{4}}-105\times {{10}^{4}}$
$\therefore {{\phi }_{E}}=67.5\times {{10}^{4}}N{{m}^{2}}/C$
Now from Gauss’s law we know that electric flux through any closed surface is $\dfrac{1}{{{\varepsilon }_{0}}}$ times the total charge enclosed. That is, if ${{Q}_{en}}$ is the charge enclosed by the closed surface, then,
${{\phi }_{E}}=\dfrac{1}{{{\varepsilon }_{0}}}{{Q}_{en}}$
$\Rightarrow {{Q}_{en}}={{\phi }_{E}}\times {{\varepsilon }_{0}}$
$\Rightarrow {{Q}_{en}}=-67.5\times {{10}^{4}}\times 8.854\times {{10}^{-12}}$
$\Rightarrow {{Q}_{en}}=-597.645\times {{10}^{-8}}C$
$\therefore {{Q}_{en}}\approx -6\mu C$
Therefore, we find that the net charge contained within the parallelepiped is negative and has a magnitude of $6\mu C$.

Note:
While finding the angle between the electric field and normal, one should be really careful. In most of the cases such as this question, the angle will not be directly given. You should note that the inclination given is that made by each face with the horizontal and you could find the required angle accordingly from it.