Question

The electric field intensity at the centre of a uniformly charged hemispherical shell is $E_{0}$. Now two portions of the hemisphere are cut from either side, and the remaining portion is shown in figure. If $\alpha=\beta=\dfrac{\pi}{3}$, then the electric field intensity at the centre due to the remaining portion is :
\[\begin{align}
  & A.\dfrac{{{E}_{0}}}{3} \\
 & B.\dfrac{{{E}_{0}}}{6} \\
 & C.\dfrac{{{E}_{0}}}{2} \\
 & D.\text{information insufficient} \\
\end{align}\]

Answer 1

Hint: Electric field is the electric force due to a unit positive charge which is at rest would exert on its surrounding. We also know that the electric potential due to a charge, is defined as the amount of energy needed to move a unit positive charge to infinity. Using the relation between the two we can solve this sum.

Formula used: $E=\dfrac{V}{r}$ and $E=-\nabla V$

Complete step by step answer:
We know that the electric force due to a pair of charges is given by Coulomb's law. An electric field can be produced by a time-varying electric field or an electrical charge. These can be either attracting or repelling in nature.
An electric field E is defined as the electric force F per unit positive charge q, which is infinitesimally small and at rest, and is given as $E=\dfrac{F}{q}$. Then $E=\dfrac{kq}{r^{2}}$, where $k=\dfrac{1}{4\pi\epsilon_{0}}$ which is a constant and $r$ is the distance between the unit charges. Since the electric field is a vector quantity, it acts along the direction of the distance $r$, then we can denote it as $\vec E=\dfrac{kq\vec r}{r^{3}}$.
Given that the electric field of the hemispherical shell as shown below is $E_{0}$. If it is cut as below, let the new electric field be $E_{1}$

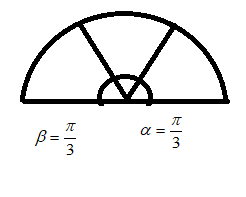
Since the electric field is a vector quantity, we can say that the vertical component of the side parts add as $2E_{1}sin(30)$ with the middle electric field $E_{1}$.
Then we can say $E_{0}=\dfrac{2E_{1}}{2}+E_{1}=2E_{1}$
$\implies E_{1}=\dfrac{E_{0}}{2}$

So, the correct answer is “Option C”.

Note: Electric field is the electric force due to a unit positive charge which is at rest would exert on its surrounding. We also know that the electric potential due to a charge is defined as the amount of energy needed to move a unit positive charge to infinity. Using the relation between the two we can solve this sum.