Question

The electric field due to a uniformly charged disc at a point very distant from the surface of the disc is given by:
($\sigma $ is the surface charge density on the disc)
A) $E = \dfrac{\sigma }{{2{\varepsilon _0}}}$
B) $E = \dfrac{\sigma }{{{\varepsilon _0}}}$
C) $E = \dfrac{{2\sigma }}{{{\varepsilon _0}}}$
D) $E = \dfrac{\sigma }{{4{\varepsilon _0}}}$

Answer 1

Hint: To solve this question, we simply have to find the electric field outside the disc. We just have to use the formulae of electric field at $x$ from the centre for a small surface and then integrate it to get the answer.

Complete step by step answer:

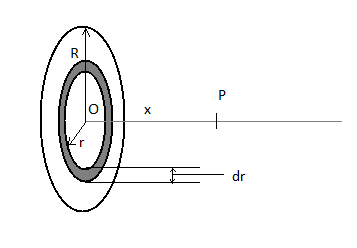
Let’s consider the disc of the radius $r$. It is given that $\sigma $ is the uniform charge density. Let $E$ be the electric field at the required point on the axis of the disc at a distance from its centre.
We have to assume the charge distribution as a collection of concentric rings of charge. Let’s consider one such ring of radius $r$ and charge $dq$.
Let a small element of area = $dA = \left( {2\pi r} \right)dr$
And the charge distribution of the ring = $dq = \sigma dA = 2\pi r\sigma dA$
Because of symmetry, there is no vertical component of the electric field at point P. So, there is only a horizontal component. We know that for a ring:
$ \Rightarrow dE = \dfrac{{k\left( {dq} \right)x}}{{{{\left( {{x^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}$
Here $x$ is the distance from the surface to the point P, $E$ is the electric field, $q$ is the charge, $r$ is the radius of the earth.
Putting the value of $dq$, we get
 $ \Rightarrow dE = \dfrac{{k\left( {2\pi r\sigma dA} \right)x}}{{{{\left( {{x^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}$
Integrating both sides,
$ \Rightarrow \int\limits_0^E {dE} = \int\limits_0^a {\dfrac{{k\left( {2\pi r\sigma dr} \right)x}}{{{{\left( {{x^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}} $
Let this be 1
Putting and differentiating we get,
$ \Rightarrow {x^2} + {r^2} = {t^2}$
$ \Rightarrow 2rdr = 2tdt$
At $r = 0$, $t = x$
At $r = a$, $t = \sqrt {{a^2} + {x^2}} $
Using this in 1, we get,
$ \Rightarrow \int\limits_0^E {dE} = \dfrac{\sigma }{{2{\varepsilon _0}}}\int\limits_x^{\sqrt {{a^2} + {x^2}} } {\dfrac{{tdt}}{{{t^3}}}} $
$ \Rightarrow E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ { - \dfrac{1}{t}} \right]_x^{\sqrt {{a^2} + {x^2}} }$
$ \Rightarrow E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\dfrac{1}{x} - \dfrac{1}{{\sqrt {{a^2} + {x^2}} }}} \right]$
$ \Rightarrow E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {\dfrac{1}{x} - \dfrac{1}{{\sqrt {{a^2} + {x^2}} }}} \right]$
$ \Rightarrow E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \dfrac{1}{{\sqrt {\dfrac{{{a^2}}}{{{x^2}}} + } 1}}} \right]$
For a very small $\dfrac{{{a^2}}}{{{x^2}}} \approx 1$
$ \therefore E = \dfrac{\sigma }{{2{\varepsilon _0}}}$
So option (A) is the correct option.

Note: Thus from the above derivation we can say that the electric field at a point due to a charged circular disc is independent from the distance of the point from the center. It depends on the surface charge density of the disc. Just like here we assumed the disc to be made up of many infinitesimally thin discs, we can use the same iea to calculate the electric field at a point due to a charged hollow cylinder.