
The effective resistance across the points P and Q is
$\begin{align}
& \text{A}\text{. }\dfrac{r}{4} \\
& \text{B}\text{. }\dfrac{r}{2} \\
& \text{C}\text{. }\dfrac{r}{8} \\
& \text{D}\text{. }\dfrac{r}{16} \\
\end{align}$

Answer
575.7k+ views
Hint: The given network can be simplified as a case of Wheatstone bridge. The potential at the points B, O, and E is the same; it means that no current will flow directly from the branch AOE. We can then redraw the network and calculate the equivalent resistance in each branch of the circuit.
Complete answer:
The equivalent resistance of a network is defined as that single resistance, which could replace the entire network in such a way that for a certain applied voltage we get the same current flowing in the circuit as we were getting for the network.
Resistances can either be arranged in series combination, or in parallel combination.
For the resistances arranged in a series combination, the equivalent resistance of the network is given by,
${{R}_{S}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+......{{R}_{n}}$
For the resistances arranged in a parallel combination, the equivalent resistance of the network is given by,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+.......\dfrac{1}{{{R}_{n}}}$
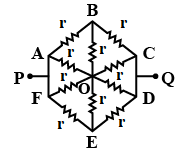
In the given figure, the points B, O, and E are at the same potential. The given network consists of two Wheatstone bridge networks connected together. The Wheatstone bridge is the name given to a network combination of four resistances connected to give a null center value.
The given circuit can be redrawn as,
Now,
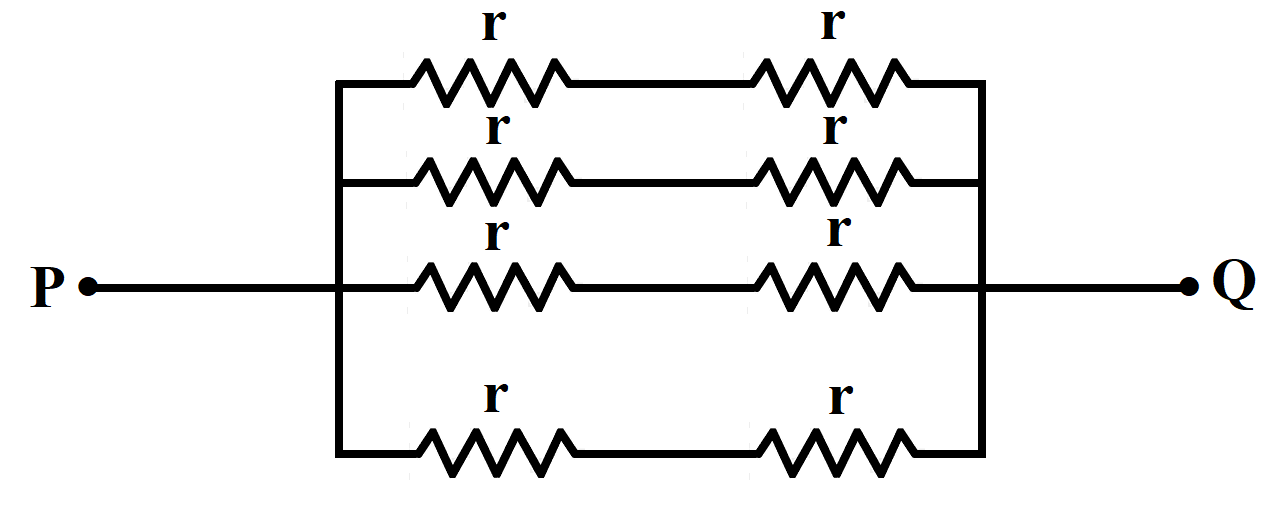
In each branch, there are two resistors in series of equal resistance value $r$
In series combination,
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$
Therefore,
In every branch, the equivalent resistance becomes,
$R=r+r=2r$
The circuit can be redrawn as,
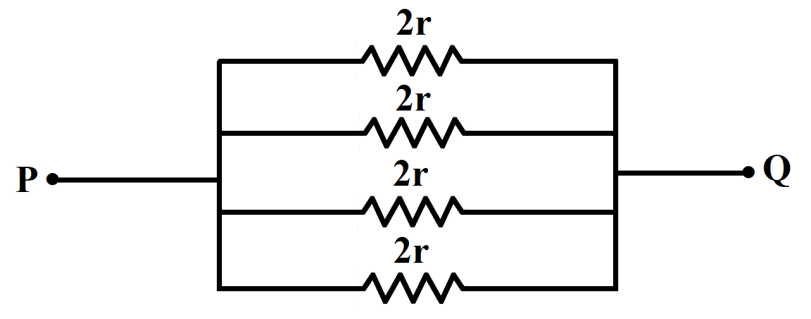
As we see, the four equal resistors in parallel combination are of equal resistance $2r$
In parallel combination,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+.......\dfrac{1}{{{R}_{n}}}$
Therefore,
The equivalent resistance P and Q becomes,
$\begin{align}
& \dfrac{1}{R}=\dfrac{1}{2r}+\dfrac{1}{2r}+\dfrac{1}{2r}+\dfrac{1}{2r} \\
& \dfrac{1}{R}=4\times \dfrac{1}{2r}=\dfrac{2}{r} \\
& R=\dfrac{r}{2} \\
\end{align}$
The equivalent circuit becomes,
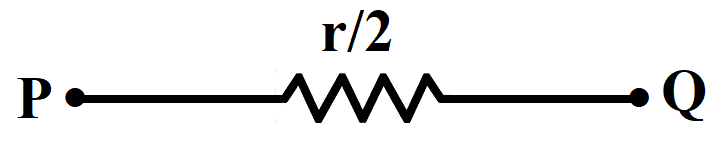
The effective resistance between the points P and Q is $\dfrac{r}{2}$
Hence, the correct option is B.
Note:
For an ohmic resistance or an effective resistance, it is insignificant whether it is connected to a direct current source or an alternating current source. In both the operating states it shows the same reaction. An electric current can flow through the resistor connected in a circuit. If the voltage is changed, the electric current flowing in the circuit is altered at the same time.
Complete answer:
The equivalent resistance of a network is defined as that single resistance, which could replace the entire network in such a way that for a certain applied voltage we get the same current flowing in the circuit as we were getting for the network.
Resistances can either be arranged in series combination, or in parallel combination.
For the resistances arranged in a series combination, the equivalent resistance of the network is given by,
${{R}_{S}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}+......{{R}_{n}}$
For the resistances arranged in a parallel combination, the equivalent resistance of the network is given by,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+.......\dfrac{1}{{{R}_{n}}}$
In the given figure, the points B, O, and E are at the same potential. The given network consists of two Wheatstone bridge networks connected together. The Wheatstone bridge is the name given to a network combination of four resistances connected to give a null center value.
The given circuit can be redrawn as,

Now,
In each branch, there are two resistors in series of equal resistance value $r$
In series combination,
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$
Therefore,
In every branch, the equivalent resistance becomes,
$R=r+r=2r$
The circuit can be redrawn as,

As we see, the four equal resistors in parallel combination are of equal resistance $2r$
In parallel combination,
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+.......\dfrac{1}{{{R}_{n}}}$
Therefore,
The equivalent resistance P and Q becomes,
$\begin{align}
& \dfrac{1}{R}=\dfrac{1}{2r}+\dfrac{1}{2r}+\dfrac{1}{2r}+\dfrac{1}{2r} \\
& \dfrac{1}{R}=4\times \dfrac{1}{2r}=\dfrac{2}{r} \\
& R=\dfrac{r}{2} \\
\end{align}$
The equivalent circuit becomes,
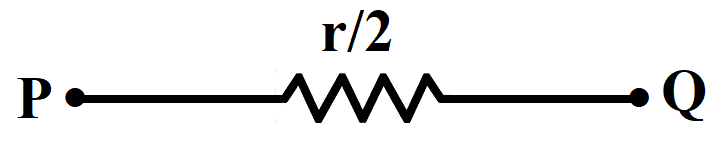
The effective resistance between the points P and Q is $\dfrac{r}{2}$
Hence, the correct option is B.
Note:
For an ohmic resistance or an effective resistance, it is insignificant whether it is connected to a direct current source or an alternating current source. In both the operating states it shows the same reaction. An electric current can flow through the resistor connected in a circuit. If the voltage is changed, the electric current flowing in the circuit is altered at the same time.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




