Question

The edge lengths of the unit cell in terms of the radius of spheres constituting FCC, BCC and simple cubic unit cell are respectively:
A. \[2\sqrt{2}r,\text{ }\dfrac{4}{\sqrt{3}}r,\text{ }2r\]
B. \[\dfrac{4}{\sqrt{3}}r,\text{ }2\sqrt{2}r,\text{ }2r\]
C. \[2r,\text{ }2\sqrt{2}r,\text{ }\dfrac{4}{\sqrt{3}}r\]
D. \[2r,\text{ }\dfrac{4}{\sqrt{3}}r,\text{ }2\sqrt{2}r\]

Answer 1

Hint: All these crystal structures have a basic cubic shape, the difference lies in the way atoms are arranged in them. All lattices have atoms present at the vertices of the cubic unit. In addition:
- In FCC, atoms are present at the centre of each face of the cubic unit.
- In BCC, only one atom is present at the very centre of the cubic unit.
- In a simple cubic unit, the only atom involved are the ones at the vertices.

Complete step by step answer:
First let us consider the simple cubic unit, it will be easier to visualize and analyze the other units once we have done this. Let us assume the edge length of the respective unit is $a$ and the radius of the atoms concerned is $r$.
i) Simple cubic unit
Atoms are present at the vertices of each cubic unit. These vertices lie at the centre of each atom. Due to the continuous and repetitive nature of crystals, each atom is shared by 8 such cubic units. Each atom contributes 1/8 parts of its volume to the cubic unit, with 8 such atoms at 8 vertices, the effective volume of one atom is present inside a cubic unit.

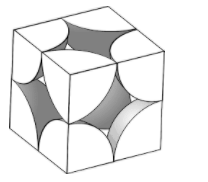
From this we can deduce that the atoms touch each other along the edges of the unit. Each edge is shared by the radii of 2 atoms. Thus, the equation for this unit will be:
\[a=2r\]

ii) Face centered cubic
Atoms are present at the 8 vertices of the cubic unit just like the simple cubic unit. Atoms will contribute 1/8 parts of their total volume. The difference here is that an atom is present at the centre of each face of the cubic unit. The centre of the atom will lie on the centre of the face. This atom will contribute 1/2 parts of its volume to the unit. Considering 6 such atoms present on each of the faces, the effective volume of atoms contained in the FCC unit will be worth 4 atoms; 3 from the atoms on the faces and one from the atoms at the vertices.

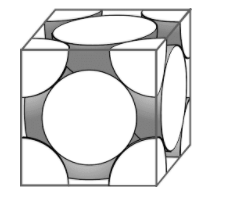
Here, we can see that the atoms touch each other along the diagonal that goes through a face of the cube. Let us call this diagonal $b$. This diagonal contains the radii of 2 atoms and the diameter of 1. Thus, the formula will be:
\[b=4r\]
Using the Pythagorean theorem and considering the fact that in a cube, all the edges have the same length we can say that:
\[{{b}^{2}}=2{{a}^{2}}\]
Substituting the value of $b$ in this equation, we get:
\[{{(4r)}^{2}}=2{{a}^{2}}\]
Solving the equation for $a$ we get:
\[a=2\sqrt{2}r\]

iii) Body centered cubic
Here, 8 atoms are present at 8 vertices of the cube and contribute a volume of 1 atom. Here the atom is present at the centre of the cubic unit and does not share its volume with any other cubic unit. It contributes its total volume to the unit. The effective volume of atoms present in the BCC lattice is 2 atoms. The centre of this atom lies on the centre of the cube.

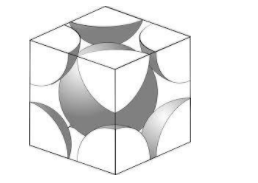
Here, we can see that the atoms touch each other along a diagonal that goes straight through the centre of the cube. Let us call this diagonal $c$. It contains the radii of 2 atoms and the diameter of 1. Thus, we get the equation:
\[c=4r\]
Now, imagine a triangle in this cube that has $c$ as the hypotenuse, $b$ as one of the sides (recall how $b$ is defined in the FCC crystal ) and $a$ as the other side. Thus, by Pythagorean theorem, we get:
\[{{c}^{2}}={{b}^{2}}+{{a}^{2}}\]
We know that, ${{b}^{2}}=2{{a}^{2}}$ substituting the values for $b$ and $c$ in the above equation, we get:
\[{{(4r)}^{2}}=2{{a}^{2}}+{{a}^{2}}\]
Solving the equation for $a$ we get:
\[a=\dfrac{4}{\sqrt{3}}r\]

Hence, the answer to this question is ‘A. \[2\sqrt{2}r,\text{ }\dfrac{4}{\sqrt{3}}r,\text{ }2r\].

Note: Remember that the $b$ defined in both FCC and BCC structures does not have the same value in terms of $r$. Only its relationship with $a$ is fixed. Do not get confused and substitute the value of $b$ that we get in FCC in the equation formulated for BCC.