Question

The earring of Ms. Shon is $5\;cm$ long. She sits in a merry-go-round moving at $4\;ms^{-1}$ in a circle of radius $2\;m$. The time period of oscillations is nearly:
A. 0.6 s
B. 0.4 s
C. 0.8 s
D. None of these

Answer 1

Hint: Try and deduce the types of acceleration that the earring is subjected to. In other words, the earring naturally experiences a gravitational acceleration but bringing in the motion of the merry-go-round lends a centripetal acceleration to the earring that is normal to gravity. Finding the resultant acceleration, and thereby using the time period equation for any periodic motion (simple pendulum) will yield the required result.

Formula used:
Time period of a simple pendulum is, in general, $T = 2\pi\sqrt{\dfrac{l}{g}}$
But in case of external factors contributing to the acceleration, $T = 2\pi\sqrt{\dfrac{l}{a_{net}}}$
Where, l is the length of the pendulum, g is the acceleration due to gravity , $a_{net}$ is the net acceleration influencing the pendulum.

Complete step by step answer:

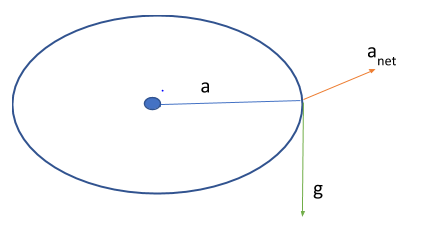
We can approximate the earing to the working of a simple pendulum.
We know that the time period of a simple pendulum is given as: $T = 2\pi\sqrt{\dfrac{l}{g}}$
This would be the case if Ms. Shon was just stationary. However, since she sits in a merry-go-round the earring, in addition to the gravitational acceleration is also subjected to a centripetal acceleration from the rotation of the merry-go-round.
This means that in order to obtain the right time period, our acceleration must be inclusive of both gravitational and centripetal forces acting on the earring.
The centripetal acceleration is given by $a = \dfrac{v^2}{r} = \dfrac{4^2}{2} = 8\;ms^{-2}$
The gravitational acceleration is numerically given as $g = 9.8 ms^{-2}$
Therefore, the net acceleration will be the resultant of the two since centripetal forces and gravity act normal to each other.
Therefore, $a_{net} = \sqrt{g^2 + a^2} = \sqrt{9.8^2 + 8^2} = \sqrt{96.04 + 64} = \sqrt{160.04} \Rightarrow a_{net}= 12.65 ms^{-2}$
Given that the length of her earring is $l =5\;cm = 0.05\;m$, the time period can be obtained as follows:
$T = 2\pi\sqrt{\dfrac{l}{a_{net}}} = 2\pi\sqrt{\dfrac{0.05}{12.65}} = 0.395\;s$
Therefore, the time period is found to be approximately $0.40\;s$
Hence the correct choice would be B. 0.4 s

Note:
Remember to calculate the resultant acceleration after including the two normal centripetal and gravitational accelerations, since discounting any one of them results in an inconsistent solution.
The centripetal force comes into play only because there is circular motion executed via the merry-go-round, and hence we can treat the entire scenario as that of a periodic circular motion.