Question

The distance of the point $P\left( 3,8,2 \right)$ from the line $\dfrac{x-1}{2}=\dfrac{y-3}{4}=\dfrac{z-2}{3}$ measured parallel to the plane $3x+2y-2z+15=0$ is
A. 7
B. 9
C. $\sqrt{7}$
D. 49

Answer 1

Hint: We are asked to find the distance from a point to the line measured parallel to a plane. To do this kind of problem in 3D, we should construct a plane parallel to the given plane $3x+2y-2z+15=0$ and pass through $P\left( 3,8,2 \right)$. The plane parallel to $3x+2y-2z+15=0$ is given by $3x+2y-2z+d=0$. By substituting P, we can get the required plane. To find the required distance, we should find the point of intersection of the new plane and the line $\dfrac{x-1}{2}=\dfrac{y-3}{4}=\dfrac{z-2}{3}$. By assuming $\dfrac{x-1}{2}=\dfrac{y-3}{4}=\dfrac{z-2}{3}=\beta $ and substituting the values of x, y, z in the new plane, we get the point of intersection B. The required distance is the distance between the point of intersection B and the given point $P\left( 3,8,2 \right)$.

Complete step-by-step answer:

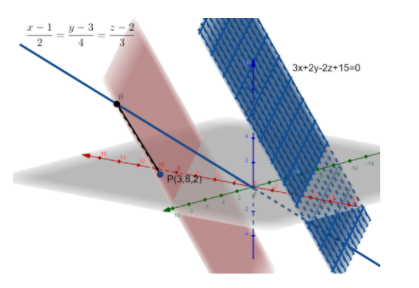
The equation of a plane parallel to $ax+by+cz+d=0$ is $ax+by+cz+{{d}_{1}}=0$.
Here, the equation of the plane is $3x+2y-2z+15=0$. In the above diagram, it is denoted by the blue surface.
Let us assume the equation of the plane parallel to the plane as $3x+2y-2z+d=0$.
We know that the point $P\left( 3,8,2 \right)$ lies on the plane $3x+2y-2z+d=0$. Let us substitute the point in the equation of the plane.
$\begin{align}
  & 3\times 3+2\times 8-2\times 2+d=0 \\
 & 21+d=0 \\
 & d=-21 \\
\end{align}$
The equation of the required plane is $3x+2y-2z-21=0$. In the diagram, it is denoted by the light cream coloured surface.
The required distance along the plane is given by the distance between the point P and the point of intersection of the line $\dfrac{x-1}{2}=\dfrac{y-3}{4}=\dfrac{z-2}{3}=\beta $ and the plane $3x+2y-2z-21=0$. It is denoted by B.
Using this equation, $\dfrac{x-1}{2}=\dfrac{y-3}{4}=\dfrac{z-2}{3}=\beta $
$\begin{align}
  & x=2\beta +1 \\
 & y=4\beta +3 \\
 & z=3\beta +2 \\
\end{align}$
Substituting the values in the plane $3x+2y-2z-21=0$.
$\begin{align}
  & 3\left( 2\beta +1 \right)+2\left( 4\beta +3 \right)-2\left( 3\beta +2 \right)-21=0 \\
 & 6\beta +3+8\beta +6-6\beta -4-21=0 \\
 & 8\beta =16 \\
 & \beta =2 \\
\end{align}$
The point B is $\left( 2\times 2+1,4\times 2+3,3\times 2+2 \right)=\left( 5,11,8 \right)$
The distance between the two points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is given by
\[\text{distance}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\]
Distance between the points P and B is
\[\text{distance}=\sqrt{{{\left( 5-3 \right)}^{2}}+{{\left( 11-8 \right)}^{2}}+{{\left( 8-2 \right)}^{2}}}=\sqrt{4+9+36}=\sqrt{49}=7\]
$\therefore $ The required distance is equal to 7 units. The answer is option-A.

Note: An alternative way is to take a parametric form of the point B. The parametric form of the point B is $\left( 2\beta +1,4\beta +3,3\beta +2 \right)$. The line PB is perpendicular to the normal of the plane $3x+2y-2z+15=0$. The directional ratios of PB are $\begin{align}
  & 2\beta +1-3,4\beta +3-8,3\beta +2-2 \\
 & 2\beta -2,4\beta -5,3\beta \\
\end{align}$
Applying the perpendicular condition, we get
 $\begin{align}
  & \left( 2\beta -2 \right)\times 3+\left( 4\beta -5 \right)\times 2+\left( 3\beta \right)\times \left( -2 \right)=0 \\
 & 6\beta -6+8\beta -10-6\beta =0 \\
 & 8\beta =16 \\
 & \beta =2 \\
\end{align}$
Using this and by calculating the perpendicular distance, we get the answer.